[강화시스터즈 2기] Min-max 알고리즘, 알파-베타 프루닝
Min-Max 알고리즘
최대 최소 전략을 사용하여 턴제 게임(체스, 바둑, 오목, 틱택토 …)등과 같은 프로그램에서 의사결정에 주로 사용되는 알고리즘. two-player 게임에서 주로 사용된다.
game: A situation in which decision-makers “Stragically interact”
- 최대 최소 전략이란? 어떤 계획이 성공했을 때의 효과를 고려하는 것보다 실패했을 때의 손실을 고려해서, 손실이 최소가 되도록 계획을 세우는 전략.
- minimize the possible loss in a worst-case scenario(”min”), maximize the potential gain(”max”)
- 두 플레이어가 있을 때, 양쪽 플레이어의 가능한 모든 행동들을 상대의 반응까지 고려해 계산하고, 가장 높은 결과값을 얻을 것으로 기대되는 최적의 행동을 선택한다.
[Player에 대한 가정]
- Rationality 합리적이다.
- 여기서 합리적이라는 것은, 각 플레이어가 일관된 선호를 갖고있다는 뜻이다. (아래를 생각하면, Max 플레이어는 항상 일관되게 자신의 score를 최대화 하는 행동을 하고, Min 플레이어는 항상 일관되게 Max 플레이어의 score를 최소화하는 행동을 해야만 한다는 것이다)
- Common knowledge of Rationallity
- 서로가 합리적으로 행동한다는 것을 너도 알고 나도 안다.
- Perfect Recall
- 플레이어는 자신이 알고 있는 정보와, 자신이 어떤 행동을 했는지 그 히스토리를 까먹지 않는다.
- 플레이어는 자신이 알고 있는 정보와, 자신이 어떤 행동을 했는지 그 히스토리를 까먹지 않는다.
-
🔍구체적인 탐색 과정
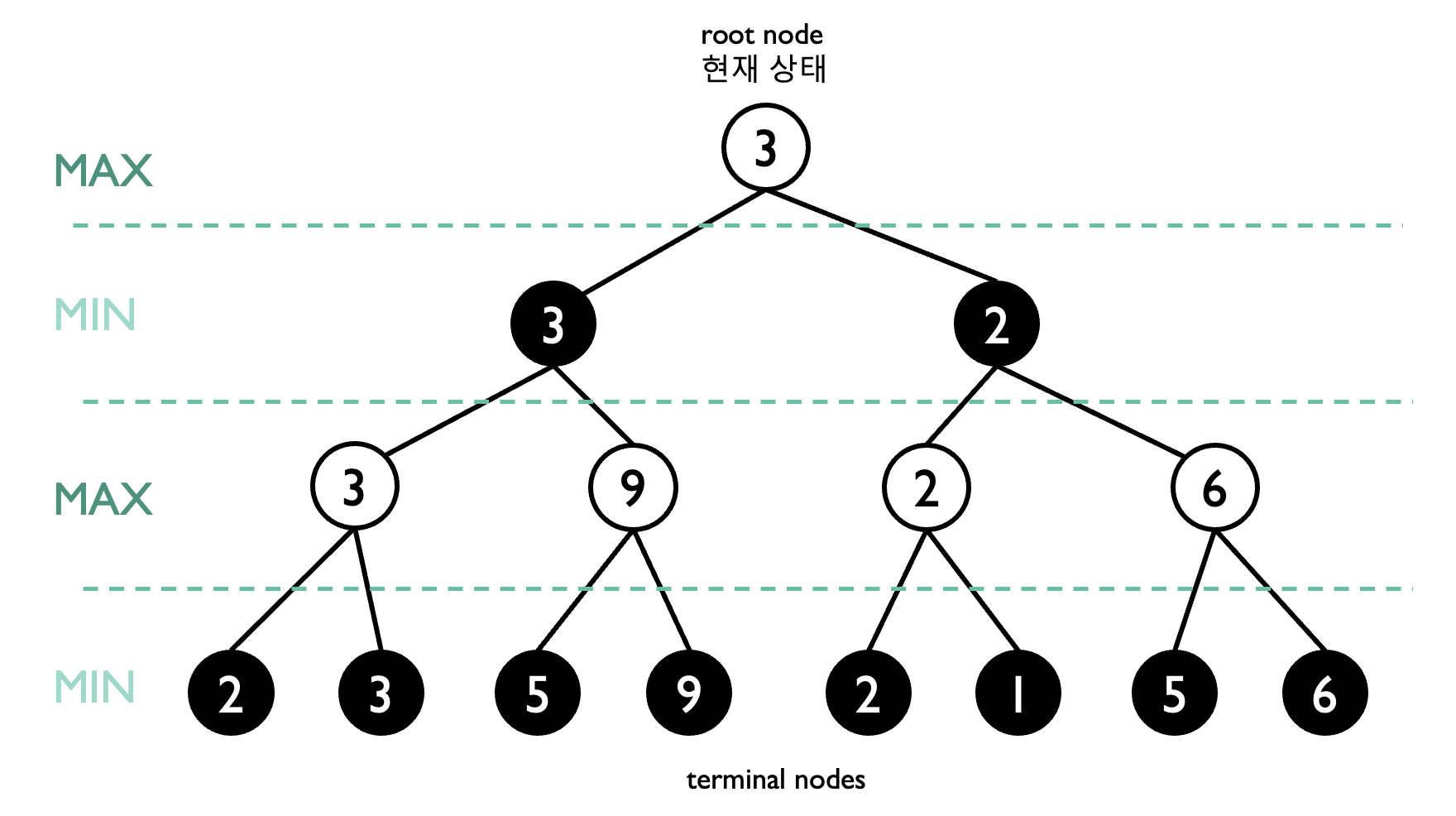
- 노드의 아래에서부터 올라가면, Max에서는 자식 노드들 중 가장 큰 값을 선택하고, Min에서는 자식 노드들 중 가장 작은 값을 선택해 표시한 것을 알 수 있다. 그리고 마지막 최상위 노드는 자식 노드들 중 최댓값을 선택한다.
- Min-Max 알고리즘의 트리 탐색 과정
- 현재 상태를 기준으로 한 층씩 내려가며 다음 수를 임의로 예상한다.
- 상태함수를 통해 각 선택에 따른 최종 결과값을 수치화한다. (terminal node들의 값)
- 수치화한 값들을 가지고, 한 층씩 올라가며 Min, Max를 반복한다.
- Min: 값을 비교하여 가장 작은 것을 선택
- Max: 값을 비교해 가장 큰 값을 선택
- 마지막 최종 선택은 Max값을 계산한다. (root node의 값)
- root node는 현재 상태이다. 현재 상태에서, 어떤 선택을 해야 가장 높은 점수를 얻을 수 있는지 계산하는 것이 게임트리이다.
-
단점: 트리의 모든 노드를 탐색해야하기 때문에 트리의 깊이가 많아질수록 계산시간이 늘어난다. 즉, 복잡한 게임을 끝까지 탐색하는 것은 불가능하다. 게다가 에이전트는 행동을 하고 다음 상태로 갈 때마다 모든 경우의 수에 대한 게임 트리를 계산하는 것을 반복하면서 최적의 행동을 한다. 상태와 행동의 개수가 늘어나면 계산량이 기하급수적으로 늘어나게된다.
-
이런 문제를 해결하기 위해?
- 휴리스틱: 어느 정도 깊이의 수까지 탐색한 후 판정
- 알파-베타 가지치기 (Alpha-beta pruning): 탐색할 필요가 없는 노드를 탐색에서 제외
이외에도 킬러 휴리스틱, 역사 휴리스틱 등의 가지 정리 방법이 존재한다.
탐색 깊이를 늘리면 더 정확한 결정을 내릴 수 있지만, 계산 시간이 기하급수적으로 증가하므로 적절한 깊이를 선택하는 것이 중요!
알파-베타 가지치기
순서대로 탐색하다가, 더이상 탐색할 필요가 없는 노드는 건너뛰어서 노드 탐색 시간을 단축한다.
알파 컷
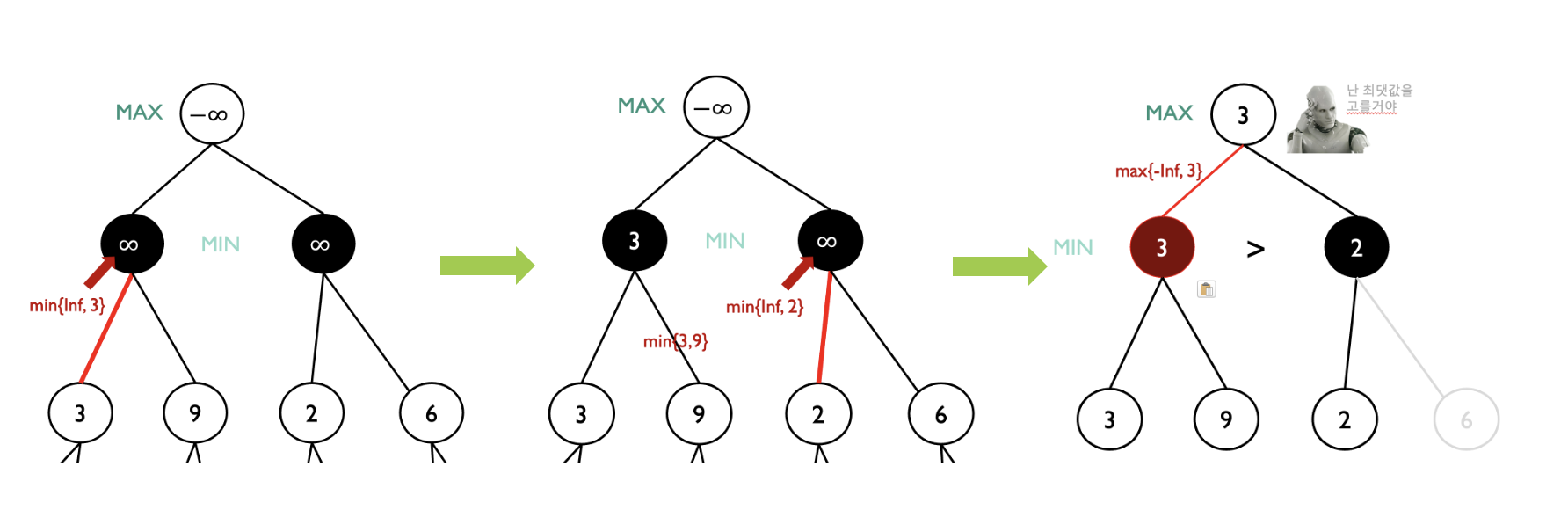
- 왼쪽에서부터 탐색한다고 가정하자. 우선 Min이 결정하는 노드의 초기값은 $\infin$로 지정한다. 왼쪽 가지를 탐색하면 왼쪽 노드의 값을 $\infin$과 3 중 작은 값으로 업데이트 한다. 오른쪽 가지에 대해서도 탐색해 왼쪽 노드의 값은 3이 되었다. 그리고 오른쪽 노드의 값을 계산한다. 왼쪽 가지를 탐색하니 오른쪽 노드의 값이 2가 되었다. 더이상 탐색하지 않아도, 왼쪽 노드의 값이 오른쪽 노드의 값보다 크다. 즉, 다음 턴에서 Max는 왼쪽 노드의 값을 취할 것이다. (오른쪽 가지를 탐색해도 오른쪽 노드의 값이 2보다 커질 리는 없다.)
베타 컷
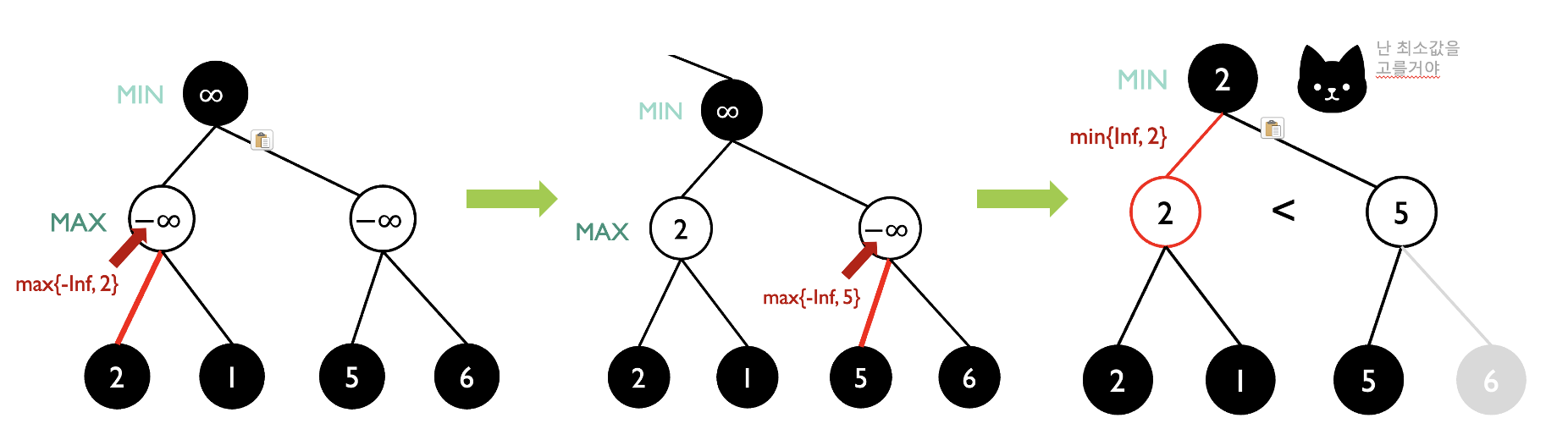
- 왼쪽에서부터 탐색한다고 가정하자. 우선 Max가 결정하는 노드의 초기값은 $-\infin$로 지정한다. 왼쪽 가지를 탐색하면, 왼쪽 노드의 값을 $-\infin$과 2 중 큰 값으로 업데이트한다. 오른쪽 가지에 대해서도 탐색하면 왼쪽 노드의 값은 2가 되었다. 그리고 오른쪽 노드의 값을 계산한다. 왼쪽 가지를 탐색하니 오른쪽 노드의 값이 5가 되었다. 더이상 탐색하지 않아도, 왼쪽 노드의 값이 오른쪽 노드의 값보다 작다. 즉, 다음 턴에서 Min은 왼쪽 노드의 값을 취할 것이다. (오른쪽 가지를 탐색해도 오른쪽 노드의 값이 5보다 작아질 리는 없다.)
노드의 순서가 중요!
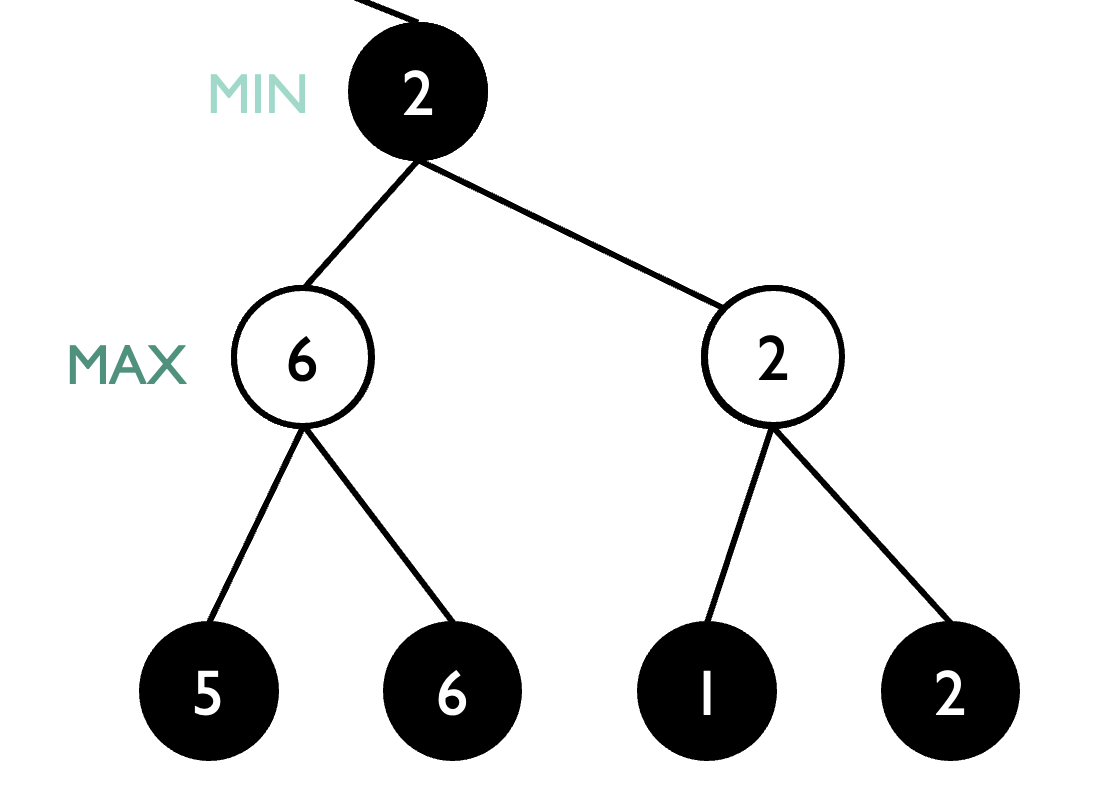
-
베타컷 예시에서, 만약 terminal node들을 이런 순서로 탐색한다면, 베타컷을 적용하지 못하고 끝까지 탐색해야한다.
-
초기값 설정의 근거?
-
Max 턴의 노드 초기값 = $-\infin$
$\max(origin_value,node_value)$의 방식으로 노드의 값을 업데이트 하기 때문이다.
-
Min 턴의 노드 초기값 = $\infin$
$\min(origin _value,node_value)$의 방식으로 노드의 값을 업데이트 하기 때문이다.
-
코드 (출처: 유튜브 영상)

그냥 Min-Max 알고리즘
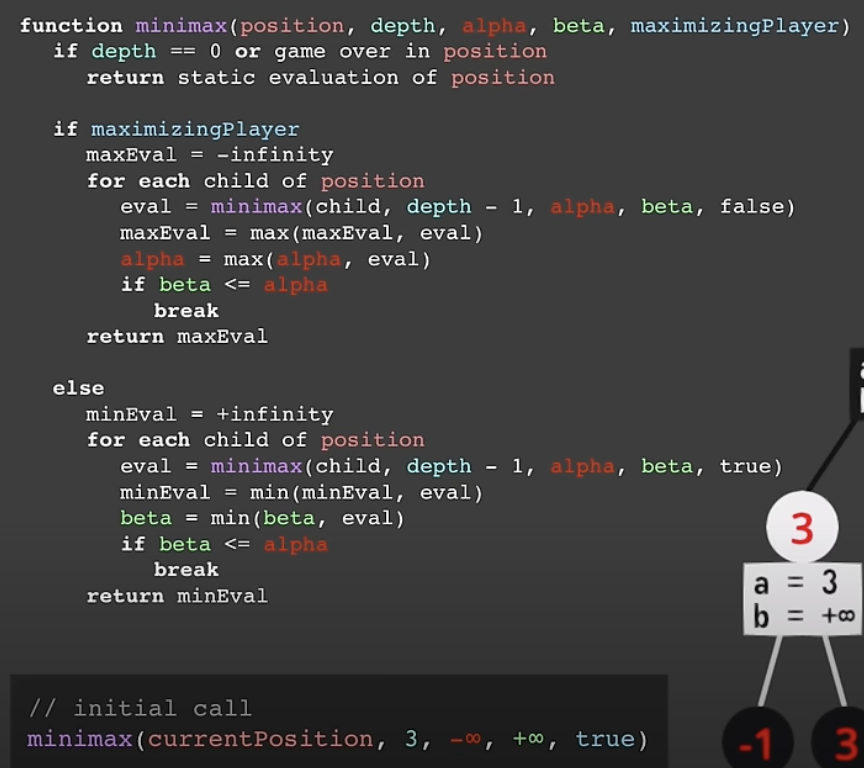
Min-Max 알고리즘 with alpha-beta pruning
[출처]
https://aboutnlp.tistory.com/18
https://www.geeksforgeeks.org/mini-max-algorithm-in-artificial-intelligence/
https://blog.naver.com/jerrypoiu/221280459884
https://www.youtube.com/watch?v=l-hh51ncgDI