30 September 2024 - 11 mins read time
이정연
Tags: 24-2 개념정리

On/off-Policy & Q-Learning

2024-09-30 이정연

On-policy 강화학습의 단점

5X5 그리드월드에서 살사(SARSA)와 $\epsilon$-탐욕 정책을 사용하여 현재 상태의 큐함수를 업데이트하는 것을 생각해보자.

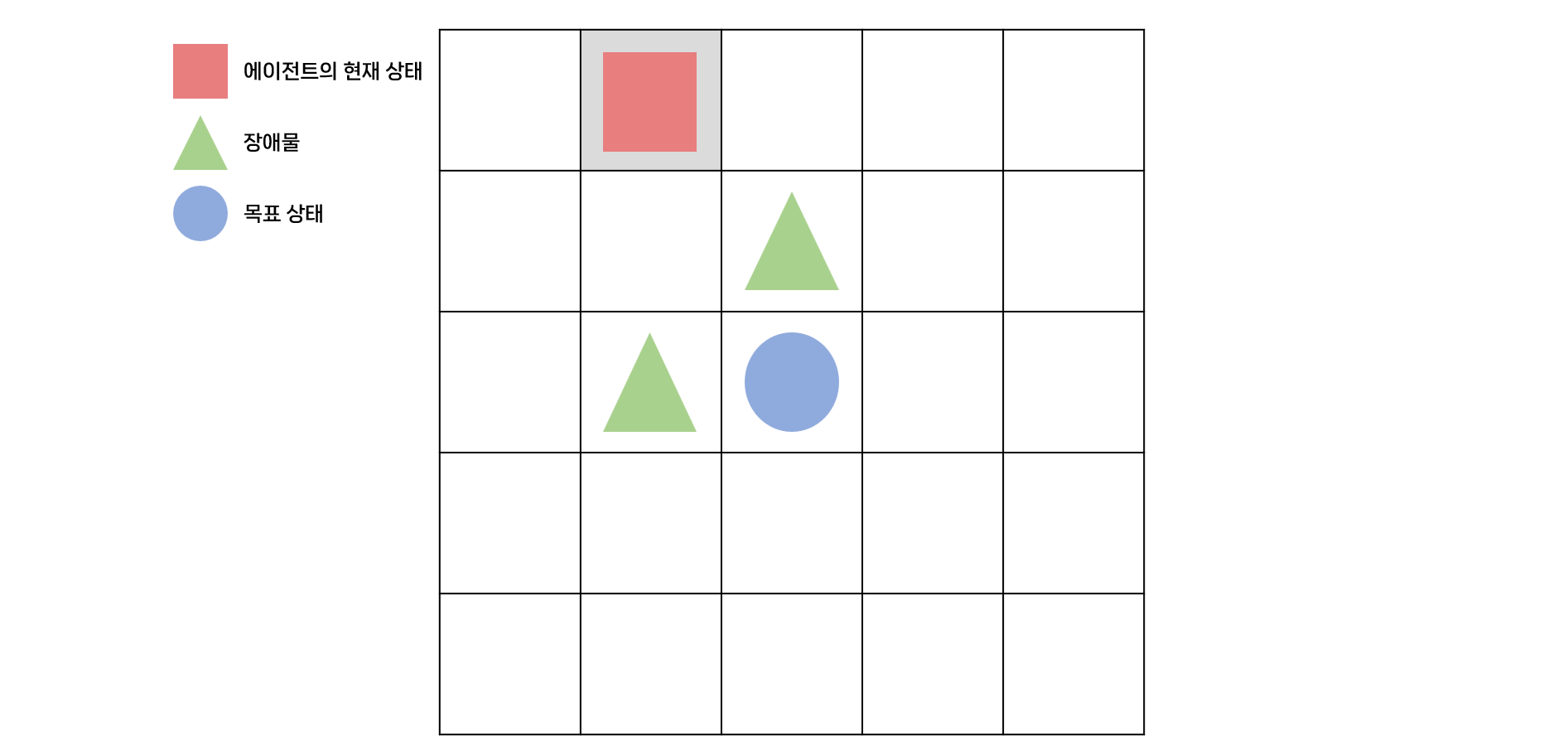
에이전트는 빨간색 네모의 현재 상태에서 탐욕 정책에 따라 큐함수가 가장 큰 행동인 오른쪽으로 가는 행동 a를 선택했다고 하자.

에이전트는 행동 a로 인해 보상 r을 받고 다음 상태 s’으로 이동한다.

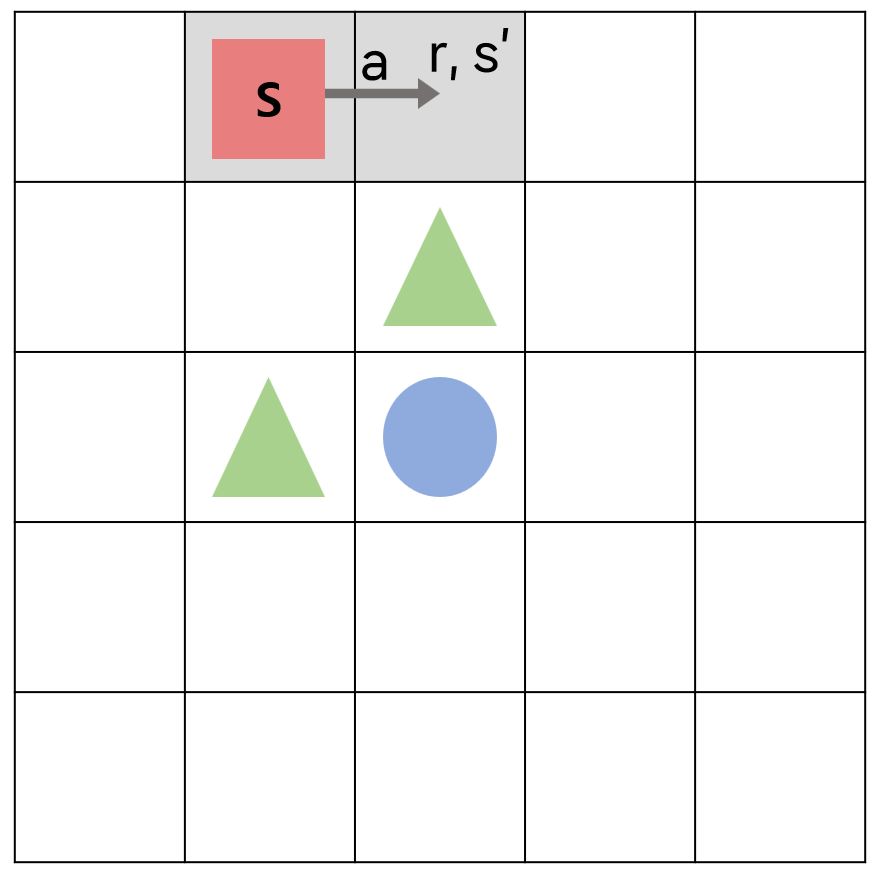
다음 상태인 s’에서 행동을 선택하는데, 이 때 난수가 $\epsilon$ 값보다 작아서 탐욕 정책이 아닌 탐험을 하게 되어 아래로 가는 행동 a’을 선택하게 되었다고 하자.

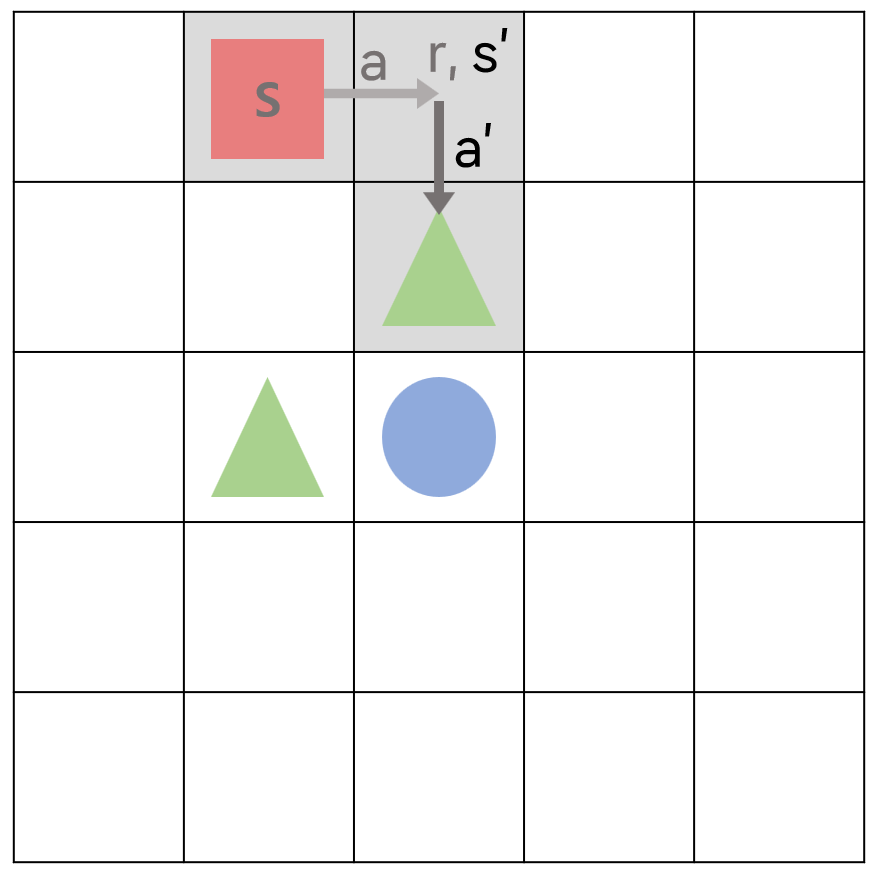
다음 행동 a’까지 한 다음에 에이전트는 {s, a, r, s’, a’}의 샘플을 이용해 큐함수를 업데이트하게 된다.

$Q(s, a)\leftarrow Q(s,a)+\alpha (r+\gamma Q(s’,a’) - Q(s,a))$

이 때 $Q(s’,a’)$은 초록색 세모(-1의 보상을 주는 장애물)로 가는 행동의 큐함수이므로 값이 낮다. 따라서 업데이트되는 현재 행동의 큐함수 $Q(s,a)$의 값은 $Q(s’,a’)$으로 인해 낮아지게 된다.

이렇게 큐함수를 업데이트하고 나서 다시 현재 상태에 에이전트가 오게 되면 오른쪽으로 가는 행동 a를 하는 것이 안 좋다고 판단하게 된다.

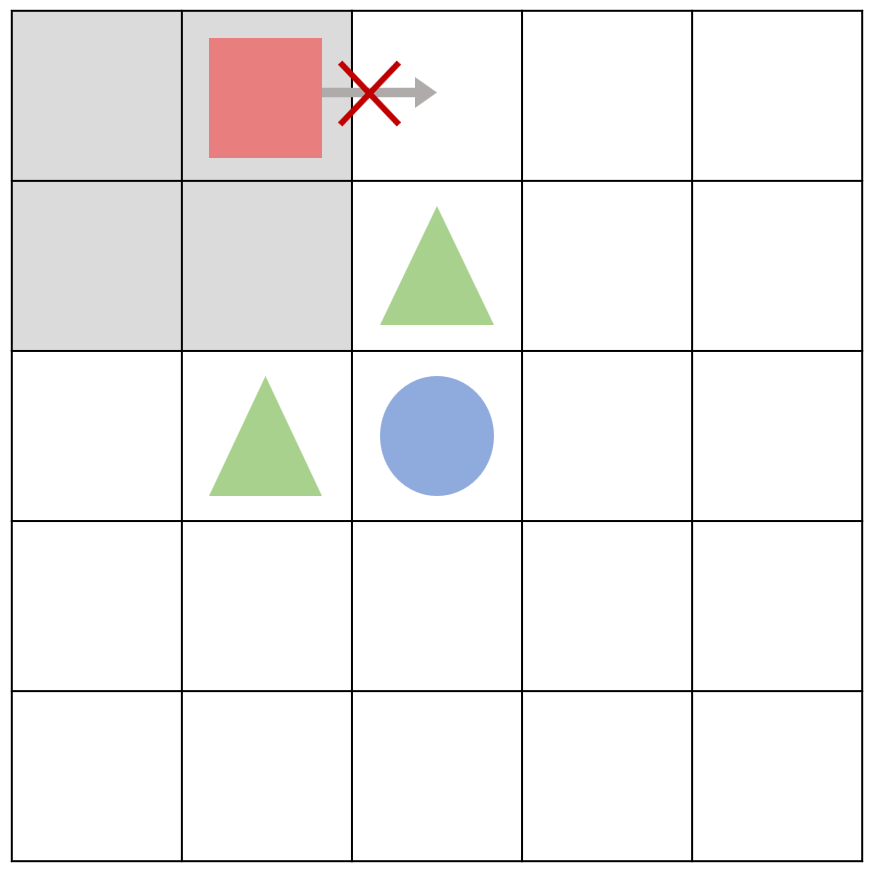
오른쪽으로 가는 행동 a에 대한 큐함수를 한 번 낮게 책정하게 되면, $\epsilon$-탐욕 정책에 의해 행동하는 에이전트는 다른 행동에 비해 낮은 큐함수 값을 가지는 행동 a를 탐욕 정책에 의해서는 절대 선택하지 않을 것이다. 따라서 에이전트가 오른쪽으로 가지 않고 위와 같이 일종의 갇혀버리는 현상이 발생하게 된다.

살사는 온폴리시 시간차 제어(on-policy temporal-difference control), 즉 자신이 행동하는 대로 학습하는 시간차 제어이다. 탐험을 하기 위해 선택한 $\epsilon$-탐욕 정책 때문에 에이전트는 한 번 잘못된 정책을 학습하면 최적 정책을 학습하기 어렵다.

하지만 여러 상태를 방문하고 다양한 행동을 해야 최적 정책을 학습할 수 있으므로 강화학습에서 탐험은 절대적으로 필수적인 부분이다. 이러한 탐험 vs. 최적 정책 학습 딜레마를 해결하기 위해서 사용하는 것이 바로 오프폴리시 시간차 제어(off-policy temporal-difference control)이다.

오프폴리시 알고리즘인 큐러닝에 대해 알아보자.

큐러닝 Q-Learning

큐러닝은 1989년에 Chris Watkins에 의해 소개된 이론이다.

큐러닝과 같은 오프폴리시 시간차 제어에서 에이전트는 현재 행동하는 정책과는 독립적으로 학습합니다. 즉, 행동하는 정책과 학습하는 정책을 분리한다. 에이전트는 행동하는 정책으로 지속적인 탐험을 하고, 이와 별개로 목표 정책을 따로 두어 학습은 목표 정책에 따라서 한다.

그리드월드 상황에서 에이전트가 현재 상태 s에서 행동 a를 $\epsilon$-탐욕 정책에 따라 선택했을 때 환경으로부터 보상 r과 다음 상태 s’을 받는 것은 살사와 동일하다.

하지만 살사에서 $\epsilon$ -탐욕 정책에 따라 다음 행동 a’까지 선택해야 그것을 학습에 샘플로 사용하는 것과 달리, 큐러닝에서는 에이전트가 다음 상태 s’을 일단 알게 되면 그 상태에서 가장 큰 큐함수를 현재 큐함수의 업데이트에 사용한다.

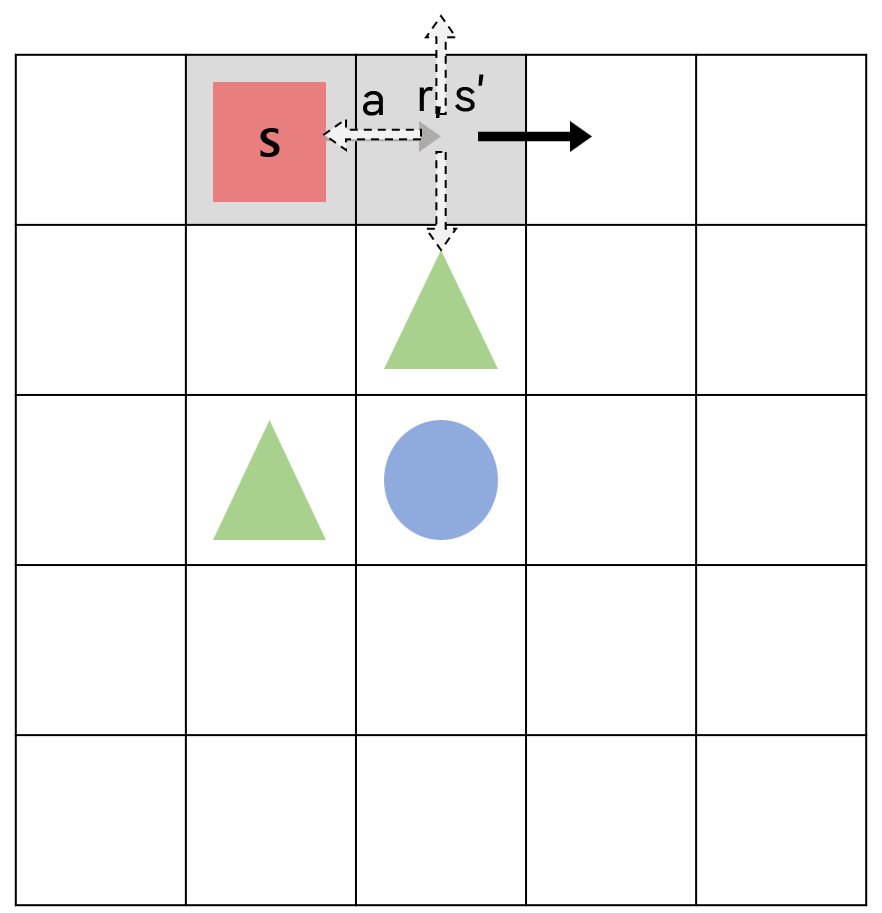
에이전트가 실제로는 다음 상태 s’에서 탐험을 통해 아래로 향하는 행동을 선택했다고 하더라도 오프폴리시 시간차 제어에서는 행동하는 정책과 학습하는 목표 정책이 분리되어 있으므로, 현재 상태에서의 큐함수는 실제 선택한 다음 행동이 아닌 최대 큐함수 값을 갖는 오른쪽으로 향하는 행동을 이용해 업데이트된다.

따라서 현재 상태의 큐함수를 업데이트하기 위해 필요한 샘플은 $<s,a,r,s’>$이다.

큐러닝을 통한 큐함수의 업데이트:

$Q(S_t, A_t)\leftarrow Q(S_t, A_t)+\alpha (R_{t+1}+\gamma \underset{a’}\max Q(S_{t+1}, a’) - Q(S_t, A_t))$

벨만 최적 방정식:

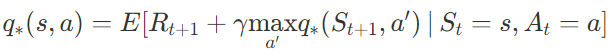
큐러닝에서 보상 $R_{t+1}$은 실제로 에이전트가 환경으로부터 받는 값이므로 큐함수 업데이트 단계에서 실제 보상 샘플을 사용하여 기댓값을 근사하는 것이므로 기댓값 $E$를 뺄 수 있고, 그러면 위의 큐러닝을 통한 큐함수 업데이트의 식과 동일하다.

$R_{t+1} + \gamma \underset{a’}\max q_* (S_{t+1},a’)$

c.f.) 살사의 큐함수 업데이트 식:

$Q(S_t, A_t)\leftarrow Q(S_t, A_t)+\alpha (R_{t+1}+\gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t))$

벨만 기대 방정식:

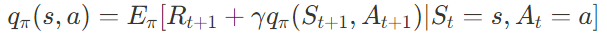
이를 통해 큐함수를 업데이트하기 위해 살사에서는 벨만 기대 방정식을 사용하고 큐러닝에서는 벨만 최적 방정식을 사용한다는 것을 알 수 있다.

살사에서의 탐험으로 인한 갇히는 문제 해결:

큐러닝을 통해 학습하면 다음 상태 s’에서 실제로 선택한 행동이 초록색 세모(장애물)로 가는 안 좋은 행동이더라도 그 정보가 현재의 큐함수를 업데이트할 때 포함되지 않는다. 왜냐하면 큐러닝에서 학습에 사용한 다음 상태에서의 행동과 실제로 다음 상태에 가서 한 행동이 다르기 때문이다.

큐러닝에서는 행동 선택은 $\epsilon$-탐욕 정책으로, 큐함수 업데이트는 벨만 최적 방정식을 이용한다.

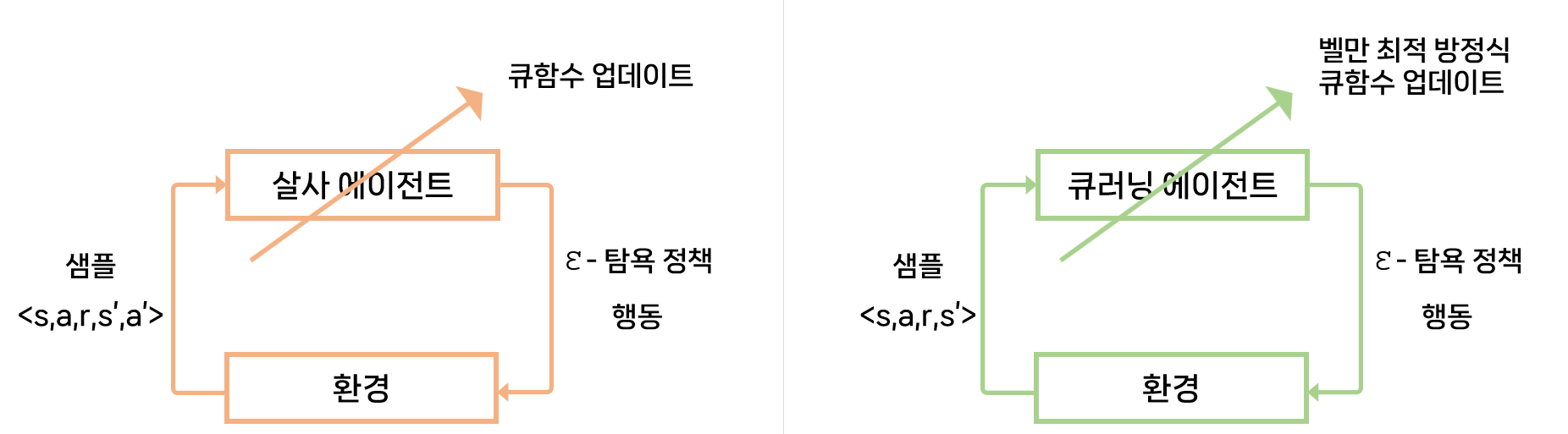
살사 에이전트, 큐러닝 에이전트의 환경과의 상호작용 비교

큐러닝 코드

import numpy as np
import random
from environment import Env
from collections import defaultdict

class QLearningAgent:
    def __init__(self, actions):
        self.actions = actions
        self.step_size = 0.01
        self.discount_factor = 0.9
        self.epsilon = 0.9
        self.q_table = defaultdict(lambda: [0.0, 0.0, 0.0, 0.0])

    # <s, a, r, s'> 샘플로부터 큐함수 업데이트
    def learn(self, state, action, reward, next_state):
        state, next_state = str(state), str(next_state)
        q_1 = self.q_table[state][action]
        # 벨만 최적 방정식을 사용한 큐함수의 업데이트
        q_2 = reward + self.discount_factor * max(self.q_table[next_state])
        self.q_table[state][action] += self.step_size * (q_2 - q_1)

    # 큐함수에 의거하여 입실론 탐욕 정책에 따라서 행동을 반환
    def get_action(self, state):
        if np.random.rand() < self.epsilon:
            # 무작위 행동 반환
            action = np.random.choice(self.actions)
        else:
            # 큐함수에 따른 행동 반환
            state = str(state)
            q_list = self.q_table[state]
            action = arg_max(q_list)
        return action

# 큐함수의 값에 따라 최적의 행동을 반환
def arg_max(q_list):
    max_idx_list = np.argwhere(q_list == np.amax(q_list))
    max_idx_list = max_idx_list.flatten().tolist()
    return random.choice(max_idx_list)

if __name__ == "__main__":
    env = Env()
    agent = QLearningAgent(actions=list(range(env.n_actions)))

    for episode in range(1000):
        state = env.reset()

        while True:
            # 게임 환경과 상태를 초기화
            env.render()
            # 현재 상태에 대한 행동 선택
            action = agent.get_action(state)
            # 행동을 취한 후 다음 상태, 보상 에피소드의 종료여부를 받아옴
            next_state, reward, done = env.step(action)
            # <s,a,r,s'>로 큐함수를 업데이트
            agent.learn(state, action, reward, next_state)

            state = next_state
            
            # 모든 큐함수를 화면에 표시
            env.print_value_all(agent.q_table)

            if done:
                break

• defaultdict : 딕셔너리의 value에 어떤 타입으로 디폴트 값을 설정할지 명시할 수 있다.

    from collections import defaultdict
      
    class QLearningAgent:
        def __init__(self, actions):
            self.actions = actions
            self.step_size = 0.01
            self.discount_factor = 0.9
            self.epsilon = 0.9
            self.q_table = defaultdict(lambda: [0.0, 0.0, 0.0, 0.0])
              
        def learn(self, state, action, reward, next_state):
            state, next_state = str(state), str(next_state)
            q_1 = self.q_table[state][action]
            q_2 = reward + self.discount_factor * max(self.q_table[next_state])
            self.q_table[state][action] += self.step_size * (q_2 - q_1)
  

  일반 딕셔너리의 경우 존재하지 않는 key 값에 접근하게 되면 에러가 발생하는데,

  defaultdict는 존재하지 않는 key 값에 대해 디폴트 value 값을 설정하는 것이 가능하다.

  → 처음으로 어떤 상태 s에서 어떤 행동 a를 했을 때의 큐함수 q_1 을 self.q_table[s][a] 값으로 하게 되면 self.q_table 의 key s 에 대한 value 값이 [0.0, 0.0, 0.0, 0.0] 으로 자동으로 설정되게 되고, 이 리스트 중 특정 행동 a를 했을 때의 값은 0.0 이 되는 것이다.

• 큐함수 업데이트

    class QLearningAgent:
        def __init__(self, actions):
            pass
               
        # <s, a, r, s'> 샘플로부터 큐함수 업데이트
        def learn(self, state, action, reward, next_state):
            state, next_state = str(state), str(next_state)
            q_1 = self.q_table[state][action]
            # 벨만 최적 방정식을 사용한 큐함수의 업데이트
            q_2 = reward + self.discount_factor * max(self.q_table[next_state])
            self.q_table[state][action] += self.step_size * (q_2 - q_1)
  

  • self.q_table[next_state] 에서 max 값을 업데이트에 사용하기 때문에 오프폴리시가 된다.
  • $Q(S_t, A_t)\leftarrow Q(S_t, A_t)+\alpha (R_{t+1}+\gamma \underset{a’}\max Q(S_{t+1}, a’) - Q(S_t, A_t))$

• 입실론 탐욕 정책에 따른 행동 선택

    class QLearningAgent:
        def __init__(self, actions):
            pass
      
        def learn(self, state, action, reward, next_state):
            pass
          
        # 큐함수에 의거하여 입실론 탐욕 정책에 따라서 행동을 반환
        def get_action(self, state):
            if np.random.rand() < self.epsilon:
                # 무작위 행동 반환
                action = np.random.choice(self.actions)
            else:
                # 큐함수에 따른 행동 반환
                state = str(state)
                q_list = self.q_table[state]
                action = arg_max(q_list)
            return action
      
    # 큐함수의 값에 따라 최적의 행동을 반환
    def arg_max(q_list):
        max_idx_list = np.argwhere(q_list == np.amax(q_list))
        max_idx_list = max_idx_list.flatten().tolist()
        return random.choice(max_idx_list)
  

  • np.amax() : 넘파이 배열 속 요소 중 가장 큰 값을 반환

    → q_list = self.q_table[state] 이므로 q_list 는 특정 state에서 가능한 행동(큐함수)의 집합이다.

    arg_max() : 탐욕 정책에 따라 max_idx_list = np.argwhere(q_list == np.amax(q_list)) 를 통해 가장 큰 큐함수를 갖는 행동의 인덱스를 모두 찾는다. 이 중 하나만 랜덤으로 반환한다.

행동하는 대로 학습하는 온폴리시의 단점을 개선하는 것이 오프폴리시이며, 대표적인 알고리즘으로 큐러닝이 있다. 오프폴리시 강화학습은 행동하는 정책과는 독립적인 목표 정책을 가지고 학습하는 것이 특징이다. 큐러닝은 행동 선택에는 $\epsilon$-탐욕 정책을 사용하고 큐함수의 업데이트에는 벨만 최적 방정식을 이용한다.

큐러닝의

행동하는 정책 : $Q(S_{t+1}, A_{t+1})$ — 선택하는 행동을 반영

학습에 이용하는 목표 정책 : $\underset{a’}\max Q(S_{t+1}, a’)$ — 다음 상태에서의 모든 행동에 대해 탐욕 정책에 따라 행동을 선택한다.

출처 : 파이썬과 케라스로 배우는 강화학습, https://00h0.tistory.com/24

Comments