08 September 2024 - 12 mins read time
이지민, 이승연
Tags: 24-2 개념정리

순차적 행동 결정 문제

• 순차적 행동 결정 문제 : (sequential decision-making problem)

강화학습에서 에이전트는 매 스텝마다 자신의 행동을 결정한다. 결정은 다음 선택에 영향을 미치기에 현재 상태는 이전 상태와 행동에 의존적이다. 이처럼 순차적으로 선택을 하고, 그 선택을 바탕으로 또 다른 선택을 하는 과정을 순차적 행동 결정 문제라고 한다. 강화학습은 순차적 행동 결정 문제를 해결하고자 고안된 하나의 방법론이다. 강화학습 이전에는 다이나믹 프로그래밍, 진화 알고리즘과 같은 방법론들이 이 문제를 해결하기 위해 사용되었다. MDP는 순차적 행동 결정 문제를 수학적으로 표현한 것이다.

마르코프 연쇄 Markov Chain

마르코프 연쇄에서 미래의 상태는 과거의 상태가 아닌, 오로지 현재의 상태에만 영향을 받는다. 다시 말해, 미래의 상태는 현재의 상태에만 종속되고, 그 이전의 상태들과는 독립이다.

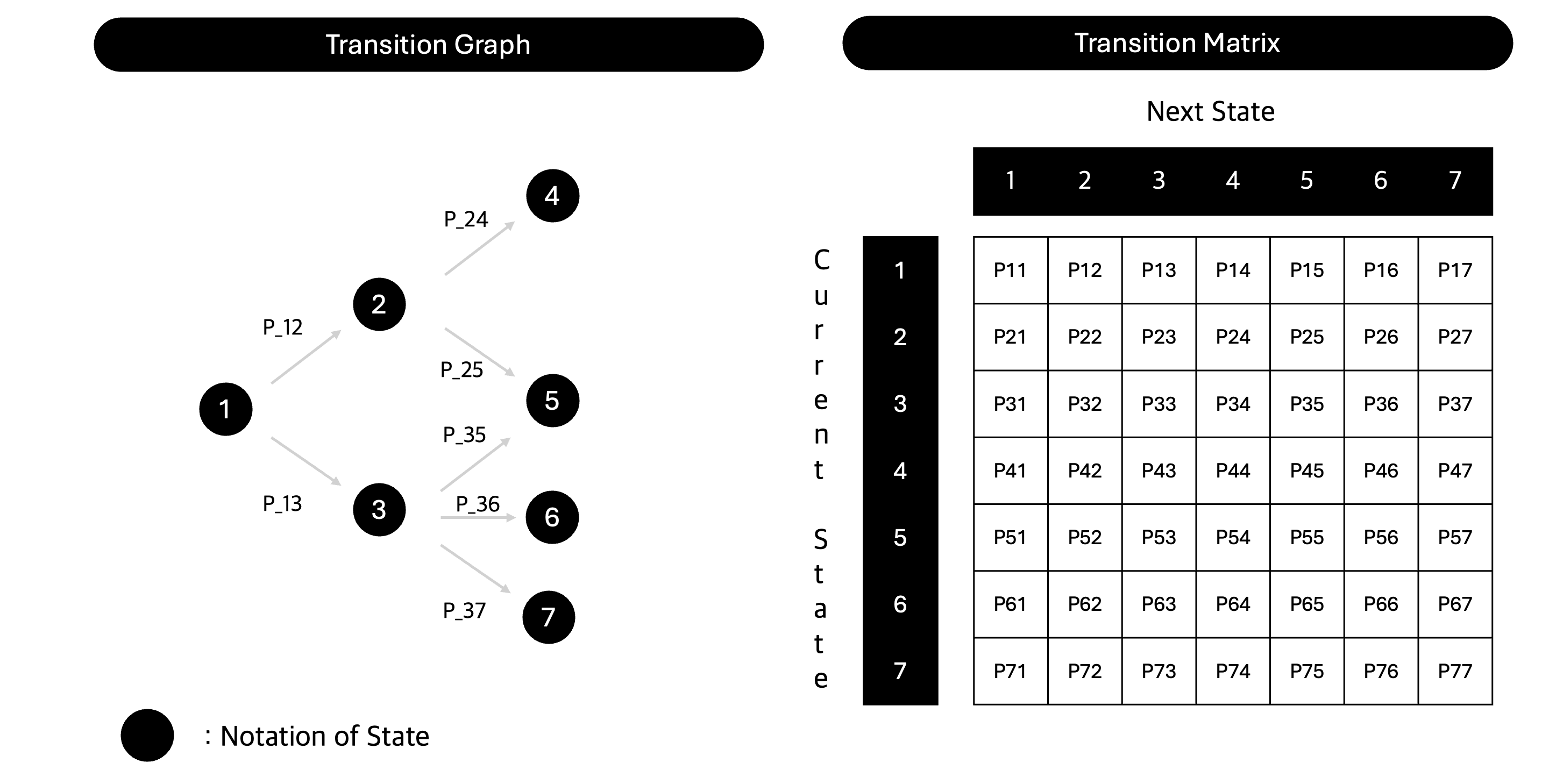
마르코프 연쇄를 수식으로 표현하면 다음과 같다.

{ ${ X_n, n=0, 1, 2, 3 … }$ } 을 이산 확률 과정( discrete-time stochastic process)이라 정의한다.

• $X_n$은 유한 이산 집합인 상태 집합 $S$의 원소를 값으로 갖는다.

[\begin{aligned} P(X_{n+1} = j | X_{n} = i, X_{n-1} = i_{n-1}, … , X_{0} = i_{0})
= P(X_{n+1} = j | X_{n} = i)
= P_{ij} \end{aligned}]

• for all $n≥0$ and $i∈S$
• $P_{ij}$ : [notation] 상태 $i$에서 상태 $j$로 갈 확률 (time step이 아닌 state 기준!)
• $Σ_{j}^{∞}P_{ij} = 1$

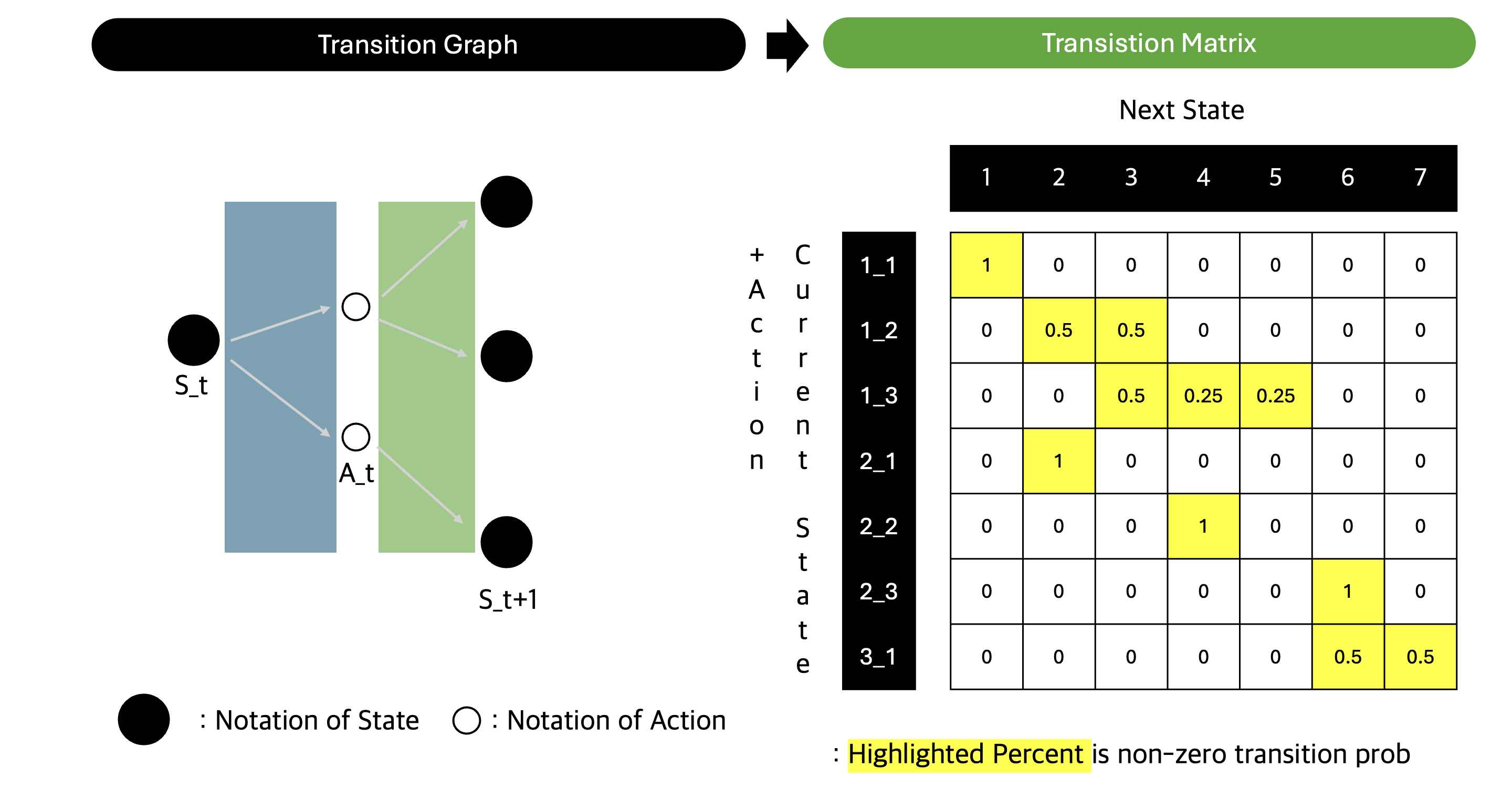
사건들이 시간 순서대로 있을 때, n+1 시점의 상태는 과거의 모든 상태와 무관하게 n번째 시점의 상태에만 영향을 받는다. 마르코프 연쇄는 상태 $i$에서 상태 $j$로 갈 확률을 정의하고, 이를 전이 확률이라 부른다. 모든 상태 사이의 전이 확률을 정리한 행렬이 전이 행렬 Transition Matrix이다.

확률 과정 Stochastic process
확률 과정은 시간($t$)에 인덱싱된 확률 변수의 집합이다.

확률 변수 random variable
확률 변수는 표본공간(Sample space) 중 랜덤으로 하나의 값을 갖는 변수다.
따라서 확률 변수는 표본 공간을 domain으로 갖는 함수라 볼 수 있다.
ex ) $S_t ∈ S$의 $S_t$는 $S$를 표본 공간으로 갖는 확률 변수로, $S$ 중 하나의 값을 랜덤으로 매 $t$ step마다 받는다.

MDP

• MDP : Markov Decision Process

순차적 행동 결정 문제에 대한 수학적 표현이자, 마르코프 연쇄의 확장판이다.

MDP는 마르코프 연쇄와 달리 행동과 행동이 좋은지 나쁜지 평가하는 reward가 추가되어, 정책으로 표현되는 제어 과정이 포함된다. 마르코프 연쇄 정의에 필요한 것이 모든 State의 집합 $S$와 전이 행렬(모든 상태에 대한 전이 확률)이라면, MDP에서 필요한 것은 상태, 행동, 보상함수, 상태 전이 확률, 할인율이다.

Markov Chain	MDP
1. 모든 State의 집합 $S$	1. 모든 State의 집합 $S$ : 상태
2. 전이 행렬(모든 상태에 대한 전이 확률)	2. 모든 Action의 집합 $A$ : 행동
	3. 보상 함수
	4. 상태 변환(전이) 확률
	5. 할인율

MDP의 구성 요소

상태, 행동, 보상함수, 상태 변환 확률, 할인율

상태 state

$S$ : 에이전트가 관찰 가능한 상태의 집합

• 상태를 표현하는 방법은 다양하다. 문제에 따라 에이전트가 학습하기에 충분한 정보를 주는 상태를 정의해야한다.

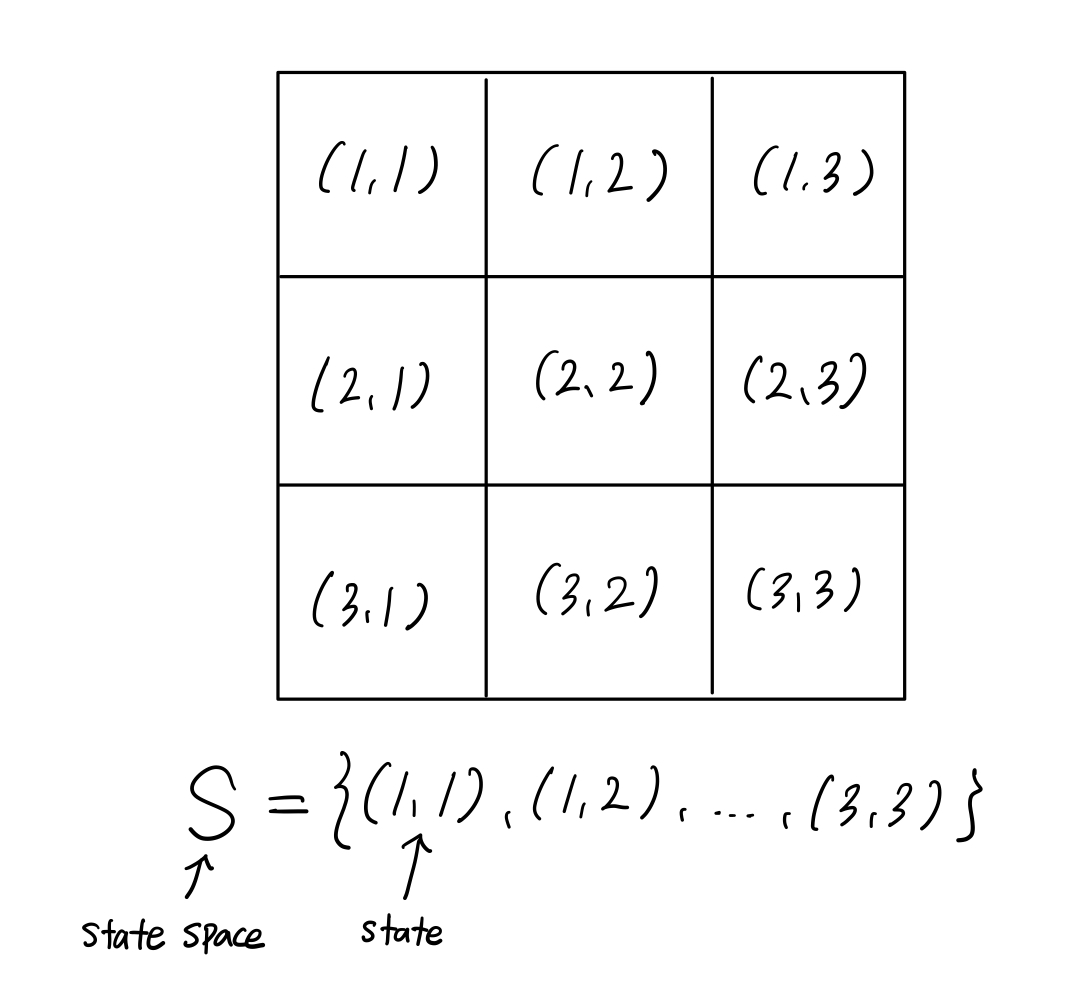
  • 그리드 월드의 경우, 상태는 좌표가 될 수 있다. ex) 3x3짜리 그리드 월드의 경우, 상태 집합 $S={ (1,1),(1,2),…,(3,3) }$

    

• $S_t=s$ : 시간 $t$에서의 상태 $S_t$가 어떤 상태 $s$이다.
  • 어떤 시간 $t$에서의 상태 $S_t$는 정해져 있지 않다. MDP에서 상태는 시간에 따라 확률적으로 변한다. 시간 t에 에이전트가 있는 상태는 전체 상태 중 하나가 될 것이다.
  • 시간 $t$에 에이전트가 있을 상태 $S_t$는 확률 변수며, 확률과정이다.

행동 action

$A$: 에이전트가 상태 $S_t$에서 할 수 있는 가능한 행동의 집합

• 일반적으로 한 문제에서 에이전트가 할 수 있는 행동들은 어떤 상태에 있든 동일하다. 즉 행동 집합 $A$가 한 문제 내에서 변하지 않는다.

• $A_t=a$: 시간 $t$에서 에이전트의 행동 $A_t$가 $a$이다.

  • 시간 $t$에 에이전트가 어떤 행동을 할 지 정해져 있지 않으니 확률 변수며, 동시에 확률과정이다.

ex) 3x3 그리드 월드

$A={up,down,left,right}$

만약 시간 t에서의 상태가 $S_t=(1,1)$이고 에이전트가 한 행동이 $A_t=right$라면, 다음 상태는 $S_{t+1}=(1,2)$이다.

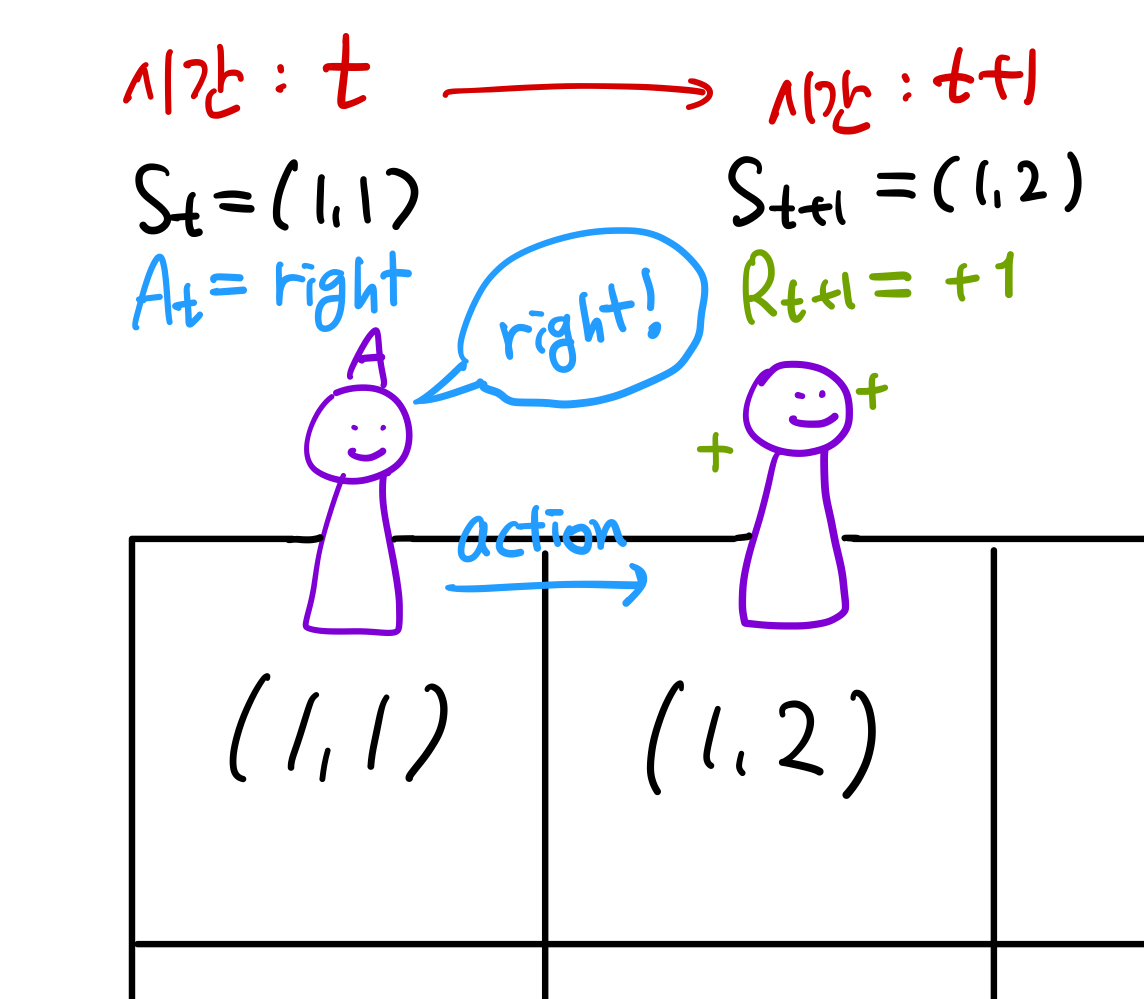
보상 reward

• 보상은 환경이 에이전트에게 주는, 에이전트가 학습할 수 있는 유일한 정보이다.

• 보상함수 (Reward function)

  \[r(s,a)=E[R_{t+1}|S_t=s,A_t=a]\]

  • 시간 $t$일 때 상태 $s$에서 행동 $a$를 했을 경우에 받을 보상에 대한 기댓값

    → 환경에 따라 같은 상태에서 같은 행동을 하더라도 다른 보상이 나올 수 있기 때문에 기댓값으로 표현한다.

  • $R_{t+1}$: 행동을 하는 시점이 $t$이고, 보상을 받는 시점이 $t+1$인 것에 주목!

    • MDP는 이산적인 환경을 전제하며, 보상은 환경이 에이전트에게 알려주는 것이기 때문이다. 에이전트가 상태 $s$에서 행동 $a$를 하면 환경이 에이전트가 가게 되는 다음 상태 $s’$과 받을 보상을 에이전트에게 알려준다. 에이전트가 시점 $t$에서 행동을 하면, 환경이 에이전트에 알려주는 것은 시점 $t+1$으로 분리된다.

상태 전이 확률

[P_{ss’}^a=P[S_{t+1}=s’

S_t=s,A_t=a]]

• 시간 $t$에서의 상태 $s$에서 행동 $a$를 했을 때, 상태 $s’$에 도달할 확률이다.
• 상태의 변화에는 확률적인 요인이 들어간다. 이 값은 환경의 일부이고, 환경의 모델(model)이라고도 부른다. 환경은 에이전트의 행동에 따라 상태 변환 확률을 통해 에이전트가 다음에 갈 상태를 알려준다.
• 마르코프 연쇄에서 상태 변환 확률이 두 상태에 의해 정의된다면, MDP에서 상태 변환 확률은 두 상태와 행동에 의해 정의된다.

할인율 discount factor

[ BG ]

강화학습은 에피소드 형식으로 학습된다. 에피소드는 유한 시간 동안 에이전트와 환경이 상호작용하며, 에피소드의 끝을 나타내는 종단 상태가 존재한다. 이때 총보상을 뜻하는 반환값 $G_t$는 종결 상태에 다다르는 시점까지 보상의 총합이다.

[G_t = R_{t+1} + R_{t+2} + … + R_T]

하지만 이렇게 반환값을 표현하는 것은 명확한 종결 시점이 없는 연속적인 상황일 때 문제가 발생한다. 시간이 무한대로 길어지면 반환값의 값 또한 무한대로 발산하기 때문이다. 이 문제를 해결하고자 할인이라는 개념을 도입한다.

할인이란, 미래 가치를 현재 가치로 환산하는 것이다. 이는 미래의 보상을 현재 시점에 미리 땡겨서 받으면 값이 더 적어진다는 개념으로, 더 미래로 갈수록 그 정도가 심해진다. 할인은 각 타임 스텝의 보상에 할인율 $\gamma$(gamma) 을 곱하는 방식으로 적용된다.

[G_t = R_{t+1} + \gamma R_{t+2} + … = \sum ^∞{k=0}\gamma ^{k-1}R{t+k}]

• 현재 시점 t로부터 k만큼의 시간이 지난 후에 받는 보상이 $R_{t+k}$이면, 현재 시점에서 보상의 가치는 $\gamma^{k-1}R_{t+k}$이다.

할인율이 [0,1]의 값임으로 무한대로 발산 하더라도 반환값은 특정 값으로 수렴한다. 이는 앞서 말했던 연속적인 문제의 보상값 발산을 해결한다. 또한 할인율은 0에 가까울수록 근미래의 반환값을 다루고, 1에 가까울수록 더 먼 미래의 보상을 더 많이 고려하는 것으로 해석할 수 있어 학습의 표현력을 높여주는 효과가 있다.

---

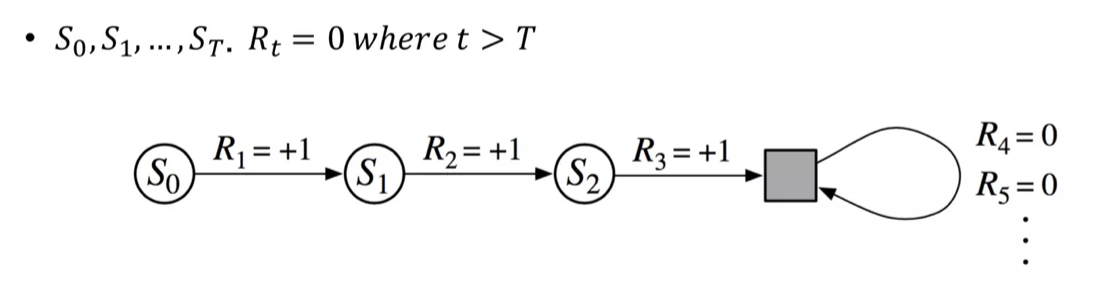
MDP의 정의

MDP는 상태, 행동, 보상, 전이 확률로 정의된다.

MDP의 핵심은 state $S_t$에서 다음 state $S_{t+1}$으로 전이될 때, 전이되는 방식이 확률적이라는 것과 그에 따른 보상이 존재한다는 것이다.

• MDP 다이나믹 함수

[P(s’,r

s,a) = Percent({S_{t+1}=s’, R_{t+1}=r

S_t=s, A_t=a})]

이 함수는 MDP의 모든 구성 요소로 이루어져 있으며 보상 함수와 전이 함수를 정의할 수 있는 발판이 된다.

---

MDP dynamic 함수로 정의하는 보상 함수와 전이 함수

1. 상태 전이 함수

   \[P(s'|s,a) = P[S_{t+1}=s'|S_t=s,A_t=a] = \sum_{r\in R}P\left( s',r| s,a\right)\]
   • 상태 전이 함수란 상태 $s$와 행동 $a$ 이후에 따라오는 상태 $s’$에 갈 수 있는 확률을 나타낸다.
   • 다시 말해, 이 함수는 상태가 전이될 때 성공할 확률이라 해석할 수 있으며, MDP의 핵심이다.

2. 보상 함수

   1. $\begin{aligned} r(s,a) &=E[R_{t+1} | S_t=s, A_t=a]
      &=\sum _{r\in R}r\sum _{s^{‘}\in S}P\left( s{‘},r| s,a\right) \end{aligned}$
   2. $\begin{aligned} r(s,a,s’) &=E[R_{t+1} | S_t=s, A_t=a, S_{t+1}=s’]
      &= \sum _{r\in R} r * P(s’,r|s,a) / P(s’|s,a) \end{aligned}$

---

MDP의 정책

정책 policy

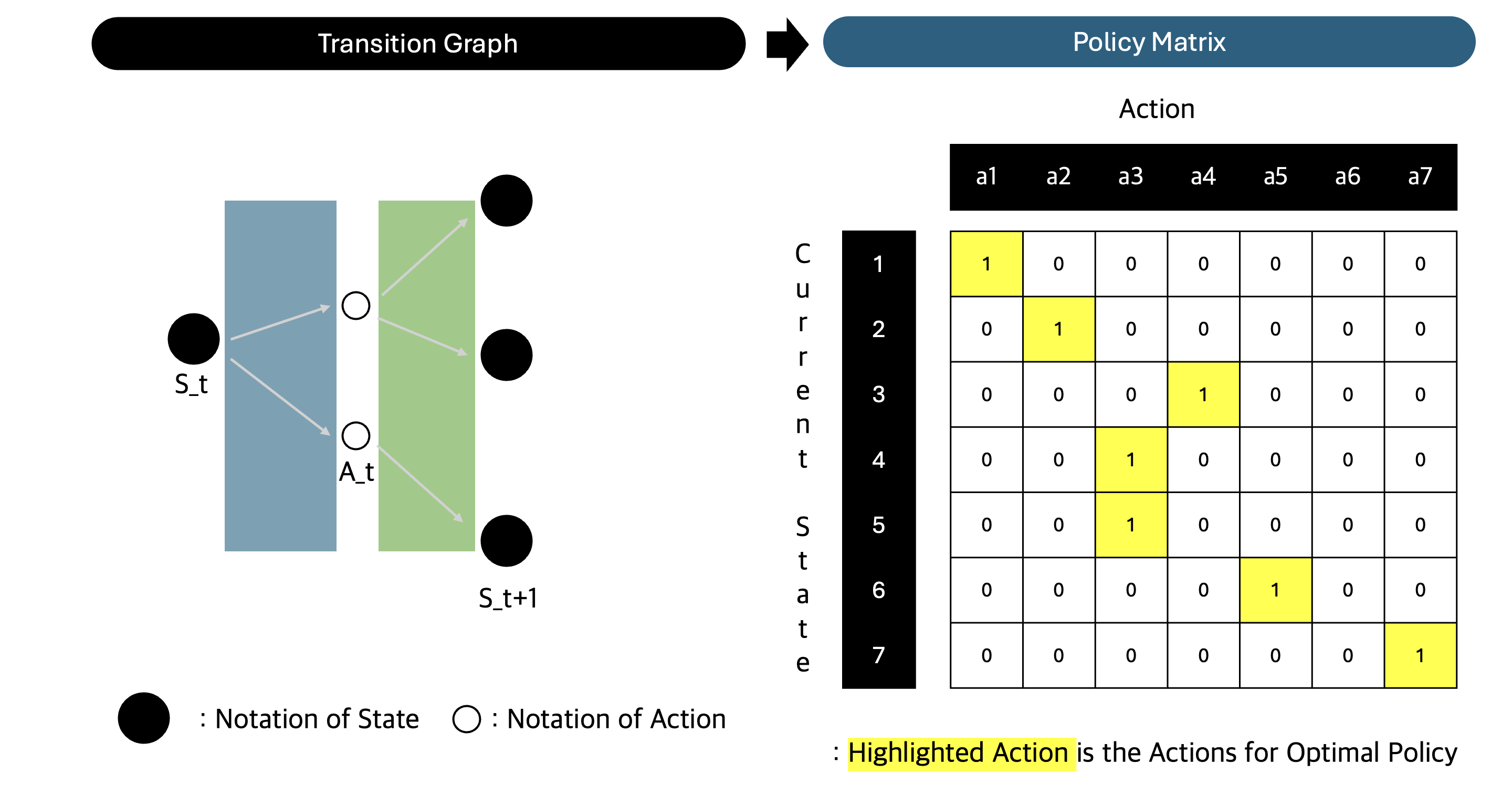
정책($\pi$)은 정책은 특정 상태에서 특정 행동을 할 확률을 정의한다. 이때 정책에서 어떤 결정을 할지 판단하는데 가치함수가 이용된다.

[\pi(a

s)=P[A_t=a

S_t=s]]

• 상태 $s$에서 행동 $a$를 할 확률을 나타낸다.

정책에서 특정 상태에 어떤 선택을 하는지는 일반적으로 탐욕적으로 정해진다. 탐욕적인(greedy) 선택은 선택지 중 가장 큰 값을 선택하는 방식이다. 따라서 정책에서 탐욕적인 선택은 모든 상태마다 가장 가치가 높은 행동을 선택하는 것을 의미한다.

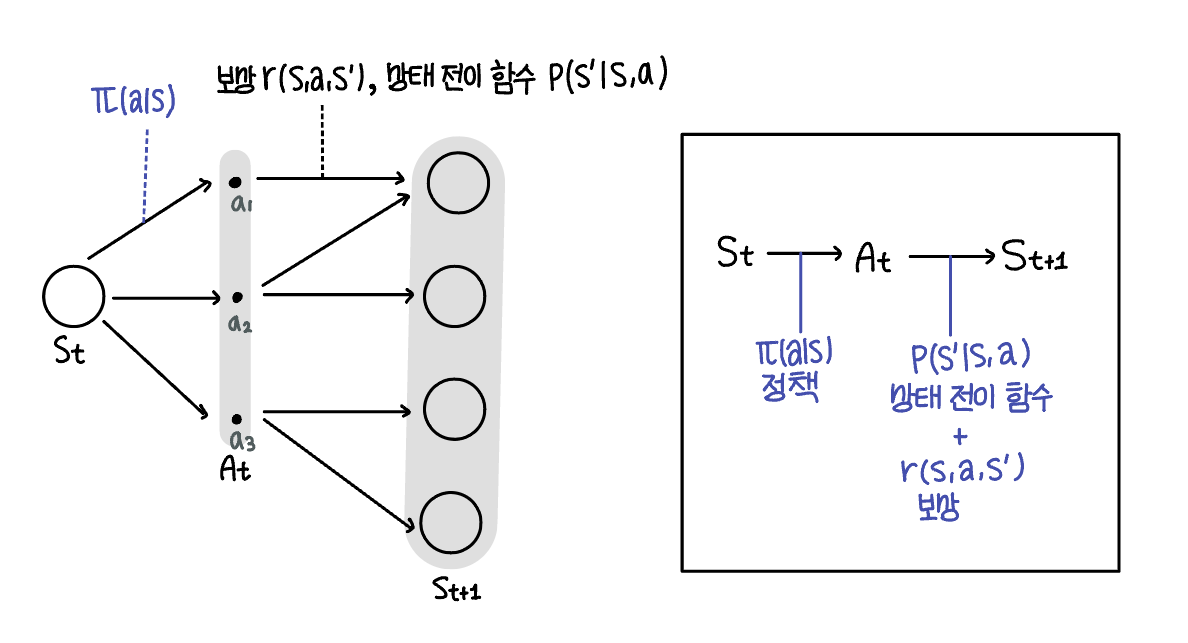
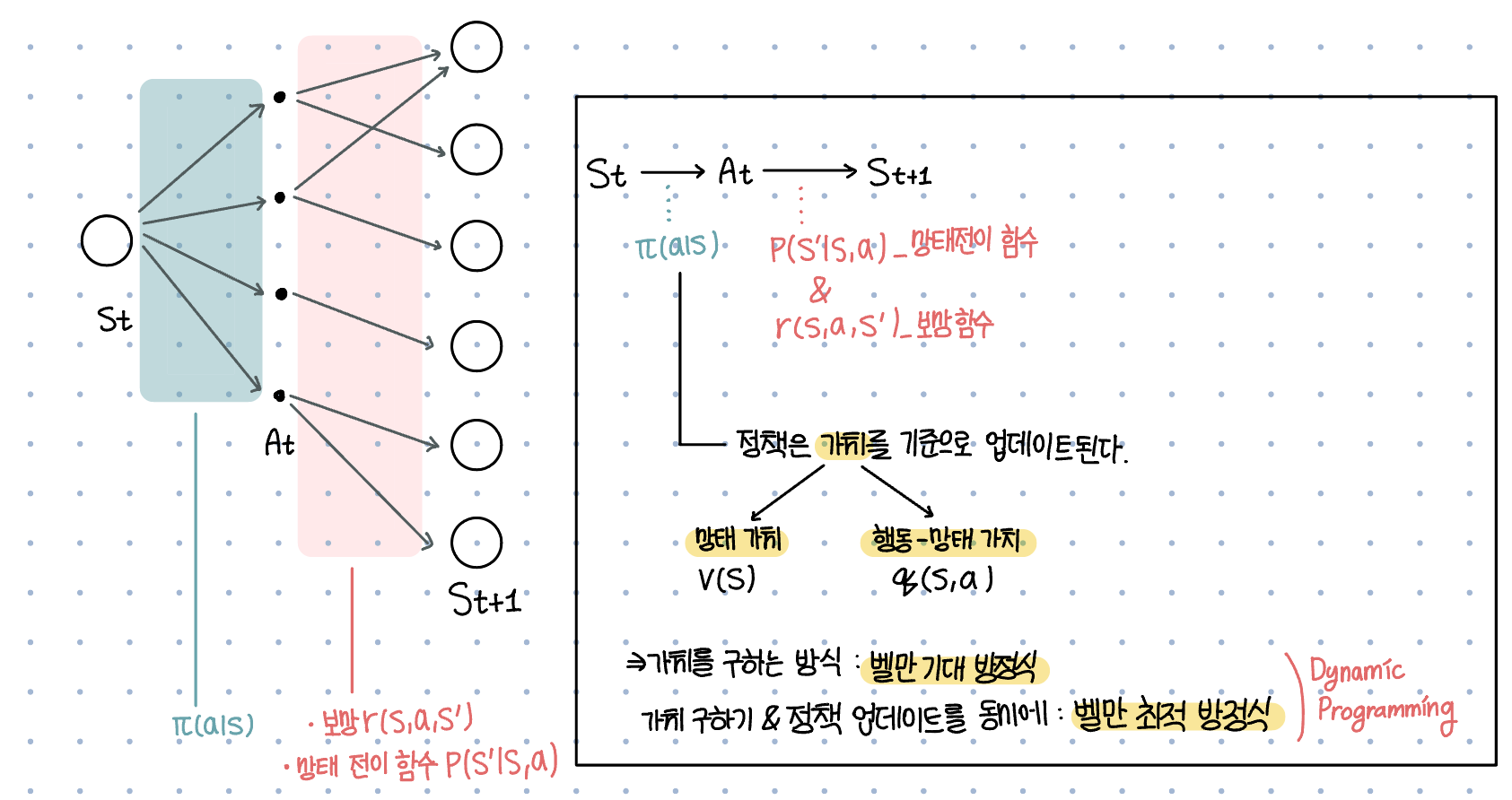
MDP 문제 : 1.정책을 통해 현재 상태에서 행동을 선택한다. 2. 상태 전이 함수를 통해 현재 상태에서 다음 상태로 확률적으로 전이된다. 3. 수행한 행동과 다음 상태를 바탕으로 보상이 에이전트에게 주어진다.

가치함수

가치 Value

가치란 특정 상태의 시작부터 일정 시간 동안 에이전트가 기대할 수 있는 보상의 총량이다. 강화학습은 최대 보상 합을 학습 목표로 하는데, 이는 최대 가치를 지니는 것과 동일하다. 또한 가치는 특정 상태가 지닌 잠재적인 보상을 내재하고 있기 때문에 장기적인 관점에서 상태의 유용성을 보여주는 단위가 된다. 따라서 일반적으로 에이전트는 보상 대신 가치를 기준으로 행동을 결정한다.

가치 함수에는 상태를 기준으로 가치를 구하는 상태 가치함수와, 상태-행동 쌍을 기준으로 가치를 구하는 행동 가치 함수가 있다.

01 상태 가치함수 state value-function

상태 가치 함수는 상태가 입력으로 들어오면 어떤 상태에서 앞으로 받을 보상의 합을 출력하는 함수다.

에이전트가 특정 상태일 때, 현 정책을 따라 향후 받게 될 보상의 합(가치)에 대한 기댓값을 출력한다.

[v : State →^{fuction} Value]

[v_{\pi}(s) = E_{\pi}[G_t

S_t=s] = E_{\pi}[\sum^∞{k=0}r^kR{t+k+1}

S_t=s]]

• 반환값 $G_t$: 시간 $t$로부터 에이전트가 행동을 하면서 받을 보상들의 현재 가치. (할인율을 적용한 보상들의 합)

  \[G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+...\]
  • 에이전트가 실제로 환경을 탐험하며 받은 보상의 합이다.
  • 에이전트는 환경과 유한한 시간동안 상호작용을 한다. 에피소드의 종단 상태에 다다르면 그때 지금까지 탐험하며 받은 보상들을 통해 반환값을 계산한다.

02 큐함수 Q-function (행동 가치함수)

큐함수는 어떤 상태에서 어떤 행동에 대한 가치를 알려주는 함수다.

에이전트가 특정 상태 - 행동을 선택할 때, 현 정책을 따라 앞으로 받을 보상의 합에 대한 기댓값을 출력한다.

[q : State,Action →^{fuction} Value]

[q_{\pi}(s,a) = E_{\pi}[G_t

S_t=s, A_t=a]]

03 가치함수와 큐함수의 관계식

정책 ${\pi}$는 상태 $s$에서 행동 $a$를 할 확률이다. 여기에 상태 $s$에서 행동 $a$의 가치인 $q_{\pi}(s,a)$를 곱한값을 상태 $s$에서 할 수 있는 모든 행동에 대해 계산해 더하면 상태 $s$의 가치함수인 $v_{\pi}(s)$ 가 된다.

[v_{\pi}(s)=\sum_{a\in A}\pi(a

s)q_{\pi}(s,a)]

왜 마르코프 연쇄와는 달리, MDP는 의사 결정 과정인가?

마르코프 연쇄 vs MDP : 정책, 가치를 중심으로

마르코프 연쇄에서 정책과 가치는 존재하지 않는다. 마르코프 연쇄는 두 상태 사이의 관계만을 정의하기 때문이다. MDP에는 행동과 행동을 평가하는 보상이 존재한다. MDP의 이 행동과 가치는 마르코프 연쇄에는 없었던 개념인 정책과 가치를 발생시켰다.

MDP에서는 가치를 통해 어떤 상태의 잠재적인 보상이 높은지를 알 수 있기에 상태의 위계가 발생한다. 최대 보상을 만들기에 유리한 상태가 있고, 그렇지 못한 상태가 존재하기 때문이다. 가치를 바탕으로 한 상태의 차등은 나에게 최대 보상을 만들어주는 선택의 집합인 정책을 만든다. 따라서 마르코프 연쇄와는 달리, MDP는 정책을 통해 제어 및 의사결정의 문제로 확장될 수 있다.

따라서 확률적인 마르코프 연쇄는 상태 집합과 전이 행렬만이 존재하지만, MDP에서는 정책과 전이 행렬이 존재한다.

벨만 방정식

벨만 방정식은 가치를 구하고자 고안된 방정식이다. 벨만 방정식은 가치 함수를 재귀 형태의 문제로 단순화시켜, 각 상태의 가치를 해당 상태에서 이동할 수 있는 상태들의 가치를 이용해 구한다.

행동 가치 함수와 상태 가치 함수는 경험으로부터 추정될 수 있다. 학습 초기 에이전트는 제대로 된 정책을 갖고 있지 않아 우변인 상태 $s$의 가치와 좌변의 값이 동일하지 않다. 여러 에피소드를 반복하며 학습하다보면, 양변 사이의 균형이 맞게 되고 모든 상태에서 균형이 안정된 가치함수를 참가치 함수라 부른다.

벨만 기대 방정식 Bellman Expectation Equation

• 상태 가치 함수

현재 상태의 가치함수 $v_{\pi}(s)$와 다음 상태의 가치함수 $v_{\pi}(S_{t+1})$ 사이의 관계를 나타내는 방정식

[v_{\pi}(s)=E_{\pi}[R_{t+1}+\gamma v_{\pi}(S_{t+1})

S_t=s]]

• 유도

  \[\begin{aligned} v(s)&=E[G_t|S_t=s]\\ &=E[R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+...|S_t=s]~~\dots(*) \\ &=E[R_{t+1}+\gamma(R_{t+2}+\gamma R_{t+3}+...)|S_t=s]\\ &=E[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_t=s] \end{aligned}\]
  • $(*)$의 식으로 계산하려면 앞으로 받을 모든 보상을 고려해야한다. 이는 상태의 개수가 많아질수록 비효율적인 방법이다. 따라서 벨만 기대 방정식의 꼴로 바로 다음 상태의 가치함수 값을 통해 현재 가치함수 값을 업데이트하는 방법으로 계산한다. 전체 경우에 대해 모두 계산하는 것보다 정확하지는 않지만, 에피소드를 충분히 반복해 샘플이 많아질수록 가치함수값은 참 값에 가까워지게 된다.

• 에이전트가 벨만 기대 방정식을 통해 가치함수를 업데이트 하는 식

  \[v_{\pi}(s)=\sum_{a\in A}\pi (a|s)(r(s,a)+\gamma v_{\pi}(s'))\]

  $ \pi (a|s)$: 각 행동에 대해 그 행동을 할 확률을 고려하고,
  $r(s,a)$ : 각 행동을 했을 대 받을 보상과,
  $\gamma v_{\pi}(s’)$ : 다음 상태의 가치함수를 고려한다.

• 벨만 기대 방정식을 통해 계속 계산을 진행하다가, 어느 순간 식의 왼쪽 항과 오른쪽 항의 값이 같아진다. 이 값이 현재 정책 $\pi$에 대한 참 가치함수 값이다.

• 행동 가치 함수 : 벨만 기대 방정식으로 표현

[q_{\pi}(s,a)=E_{\pi}[R_{t+1}+\gamma q_{\pi}(S_{t+1},A_{t+1})

S_t=s, A_t=a]]

벨만 최적 방정식 Bellman Optimal Equation

• 최적 정책 $\pi^*$: 가장 가치가 높은 행동을 선택하는 정책
  • 에이전트가 강화학습을 통해 학습해야 하는 것이 최적 정책이다.
  \[∀ s \in S,~~ v_{\pi^{*}}(s) ≥ v_{\pi}(s) → \pi^* ≥ \pi ⇒ \pi^*~is~Optimal~Policy\]
• 최적 가치함수 $v^*(s)= \max_{\pi} [v_{\pi}(s)]$: 최적 정책에 대한 참 가치함수
• 최적 큐함수 $q^*(s,a)=\max_{\pi}[q_{\pi}(s,a)]$: 최적 정책에 대한 큐함수
  • 최적 가치함수는 가장 높은 가치 함수(실질적으로 큐함수)를 찾은 경우, 각 상태의 최적 큐함수 중 가장 큰 큐함수를 가진 행동을 선택한다.
  • 최적 가치함수 또한 어떤 상태에서의 행동들 대해 최적 큐함수 중에서 최대 큐함수를 선택하는 것이 최적 가치함수이다.
• 상태 가치 함수에 대한 벨만 최적 방정식

[\begin{aligned} v^(s)&=\max_a[q^(s,a)|S_t=s,A_t=a]
&=\max_a E[R_{t+1}+\gamma v^*(S_{t+1})|S_t=s,A_t=a] \end{aligned}]

• 큐함수에 대한 벨만 최적 방정식

  \[q^*(s,a)=E[R_{t+1}+\gamma \max_{a'}q^*(S_{t+1},a')|S_t=s,A_t=a]\]

벨만 기대 방정식 vs 벨만 최적 방정식

벨만 기대 방정식은 모든 상태에 대한 가치를 계산할 뿐, 방정식 내에서 정책을 개선하지 않는다. 벨만 기대 방정식을 사용해 가치 계산 및 최적 정책을 구하는 과정은 다음과 같다. 벨만 기대 방정식을 통해 구한 각 상태의 가치에 따라 현 정책을 평가하고, 수정된 정책을 기반으로 다시 상태의 가치를 계산한다. 이 과정을 더 이상 수정되지 않는 정책을 얻을 때까지 반복한다.

그에 반해 벨만 최적 방정식은 큐함수를 기반으로 각 상태에서 가장 높은 가치를 갖는 행동을 구한다. 이는 최대 가치를 낼 수 있는 상태-행동 쌍을 찾는 것과 동일하며, 결과적으로 정책을 찾는 과정이라 볼 수 있다. 벨만 최적 방정식은 벨만 기대 방정식과 달리 가치, 정책 업데이트를 동시에 진행하기에 더 효율적인 알고리즘이다.

벨만 방정식을 통한 MDP 해결

벨만 방정식을 통해 MDP 문제를 해결하는 것은 수학적인 완결성이 보장된다는 장점이 있다. 벨만이 이 방정식을 풀기 위해 고안한 것이 바로 다이나믹 프로그래밍이다. 하지만 벨만 방정식을 풀어 MDP 문제를 해결하는 것은 효용이 아주 낮다. 모든 가능성을 내다보고 그 가능성의 발생 확률을 계산하며, 보상의 기댓값 측면에서 얼마나 좋은지를 계산하는 빈틈없는 탐색이기 때문이다. 또한 이 방식은 3가지 조건을 충족해야 지만 계산될 수 있다.

1. 환경의 구조를 명확하게 알아야 한다.

2. 전체를 계산할만큼 충분한 계산 능력을 가져야 한다.

3. 마르코프 성질을 가정해야 한다.

하지만 일반적인 케이스에서 이 세 가지 조건을 전부 충족시키는 것은 불가능에 가깝기에, 근사적인 해를 찾는 방향으로 접근하는 강화학습이 순차적 문제 해결에 더 많이 사용되고 있다.

다이나믹 프로그래밍 vs 강화학습
1. 다이나믹 프로그래밍 : 3가지 조건이 충족되는 상황에서 벨만 방정식을 통해 가치 함수를 계산하는 방법론
2. 강화학습 : 근사적으로 가치 함수를 찾는 방법론

총정리

Comments