[강화시스터즈 1기] DEEP 강화학습 방법론
아이디어 💡
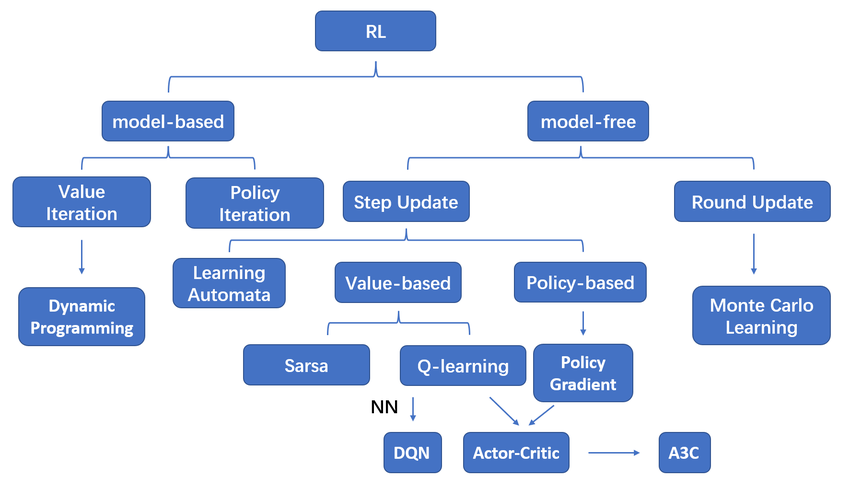
몬테카를로, SARSA, Q-러닝의 한계
몬테카를로, SARSA, Q-러닝은 에피소드를 반복하며 가치를 근사한다. 또한 다이나믹 프로그래밍과 마찬가지로 모든 상태-행동에 대한 가치를 저장하는 가치 테이블이 존재한다. 이런 테이블 형식의 강화학습은 상태 집합이 명확하게 정해져 있고, 상태 개수가 적을 때에만 적용가능하다. 따라서 셀 수 없이 많은 상태가 존재하는 테스크는 이런 테이블 형식의 강화학습 기법으로 해결할 수 없다.
딥러닝 신경망을 적용하는 강화학습 기법은 상태-행동 쌍에 대한 가치나 정책을 신경망을 통해 근사적으로 구한다. 이 방식은 모든 상태와 행동 쌍에 대한 정보를 저장할 필요가 없고, 이론적으로 모든 상태의 행동가치를 찾을 수 있어 테이블 형식의 강화학습의 문제를 해결한다.
테이블 형식의 강화학습 → Deep RL
Deep RL
강화학습에서 딥러닝이 대체하는 부분은 정책과 가치 함수다. 가치 함수를 딥러닝으로 대체해 가치를 근사적으로 구하는 방법론은 가치 그래디언트, 정책을 딥러닝으로 근사하는 것은 정책 그래디언트다.
가치 그래디언트
가치 그래디언트에서 딥러닝 신경망은 가치 함수의 역할을 수행하며, input인 각 상태에 대한 가치를 추정한다. 대표적인 가치 그래디언트에는 SARSA의 가치 함수를 신경망으로 대체하는 Deep SARSA가 있다.
- input 확인
가치 그래디언트에서 딥러닝 신경망은 가치 함수의 역할을 수행하며, input인 각 상태에 대한 가치를 추정한다. 대표적인 가치 그래디언트에는 SARSA의 가치 함수를 신경망으로 대체하는 Deep SARSA가 있다.
Deep SARSA
딥살사는 SARSA 방법론에서 가치함수를 신경망으로 근사해 최적 함수를 찾는다.
SARSA의 업데이트
SARSA의 가치 업데이트는 아래와 같은 방법으로 이뤄진다.
$𝑄(𝑠,𝑎) ← 𝑄(𝑠,𝑎) + 𝛼(𝑅_{𝑡+1} + 𝛾𝑄(𝑠’,𝑎’) − 𝑄(𝑠,𝑎))$
SARSA는 $𝑅_{𝑡+1} + 𝛾𝑄(𝑠’,𝑎’)$를 일시적인 정답값으로 해석하고, 현재 추정한 Q함수 값과 $𝑅_{𝑡+1} + 𝛾𝑄(𝑠’,𝑎’)$값 사이의 오차를 가치 업데이트에 사용하며 상태에 대한 최적 가치를 구하고자 한다.
DeepSARSA : 신경망 정보
딥러닝은 정답값과 예측값 사이의 오차를 줄여나가며, 궁극적으로 global minima에 도달하고자 한다. 딥살사도 딥러닝과 마찬가지로 일시적 정답 역할을 하는 $𝑅_{𝑡+1} + 𝛾𝑄(𝑠’,𝑎’)$와 pred인 $𝑄(𝑠,𝑎)$ 사이의 오차를 줄이며 학습한다.
오차를 줄여나가는 과정임으로 경사 하강법이 이용되며, 오차값 계산을 위해 일반적으로 MSE를 사용한다.
| DEEP LEARNING | DEEP SARSA |
|---|---|
| 정답 | $𝑅_{𝑡+1} + 𝛾𝑄(𝑠’,𝑎’)$ |
| 예측값 | $𝑄(𝑠,𝑎)$ |
| loss function | $MSE = (ans - pred)^2 = (𝑅_{𝑡+1} + 𝛾𝑄(𝑠’,𝑎’) − 𝑄(𝑠,𝑎))^2$ |
| nn의 역할 | 가치함수 |
| nn의 input | 상태 |
| nn의 output | input 상태에 대한 가치 |
| num of output layer’s node | num of actions |
$Q_{\theta}(S_t,A_t) ← Q_{\theta}(S_t,A_t) + \alpha (𝑅_{𝑡+1} + 𝛾𝑄_{\theta}(𝑠_{t+1},𝑎_{t+1}) − 𝑄_{\theta}(𝑠_t,𝑎_t))^2$
정책 그래디언트
정책 그래디언트는 신경망을 통해 정책을 근사한다. 따라서 가치 그래디언트와는 달리, 신경망의 ouput layer은 각 행동을 할 확률을 근사한다. 또한 가치에 따라 탐욕적인 선택을 하는 일반적인 정책과 달리, 정책 그래디언트는 가치를 거치지 않고 신경망으로 정책을 근사하기 때문에 가치를 구할 필요가 없다.
정책 $\pi_{\theta}(a|s)$
$\theta$는 nn의 파라미터로, 정책이 신경망의 파라미터로 정해짐을 의미한다.
정책 그래디언트의 학습 목표
정책 그래디언트는 최적 정책을 찾고자 한다. 최적 정책은 최종 보상의 합이 최대가 되는 모든 상태-행동 쌍이 정의된 정책이다. 따라서 정책 그래디언트의 신경망은 상태를 입력받았을 때, 누적 보상을 최대로 만드는 행동을 뱉는 것을 목표로 한다.
이 상황을 수식으로 정리하면 아래와 같다.
- 학습 목표 : $maxJ(\theta)$
- $J(\theta)$ : 누적 보상
- $J(\theta) = v_{\pi_{\theta}}(s_0)$
- 누적 보상을 상태 $s_0$에 대한 가치로 표현할 수 있는 이유?
- 정책 그래디언트 업데이트
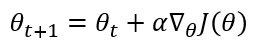
가치 그래디언트는 현재 추정한 Q함수 값과 $𝑅_{𝑡+1} + 𝛾𝑄(𝑠’,𝑎’)$값 사이의 오차를 줄이는 방향으로 학습하기에 경사 하강법을 이용하지만, 정책 그래디언트는 누적 보상인 $J(\theta)$의 최대값을 찾고자하기 때문에 경사 상승법을 이용한다.
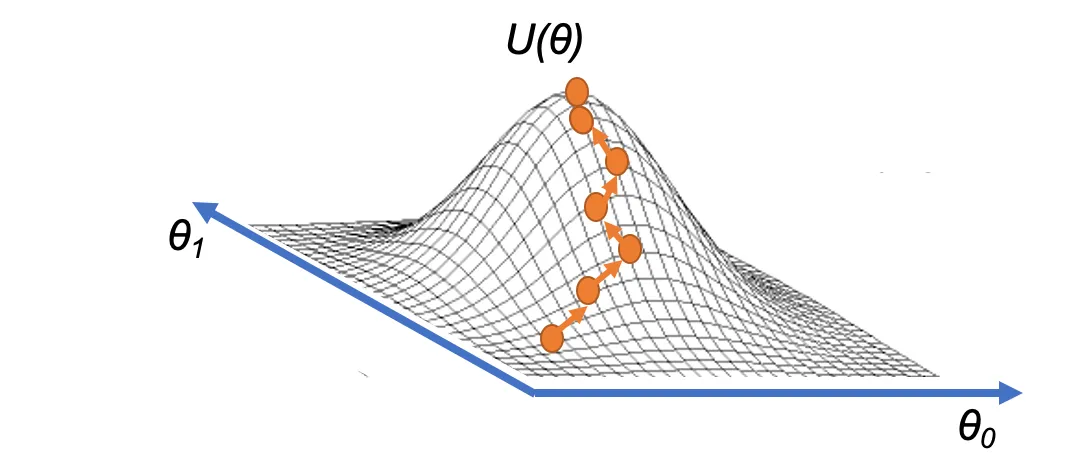
경사상승법을 시각화 : 이미지에서 $U(\theta)$로 표현된 값이 $J(\theta)$다.
경사 상승법을 업데이트하기 위해서는 누적 보상 함수 $J(\theta)$의 그래디언트를 알아야 한다.

Policy Gradient Methods for Reinforcement Learning with Function Approximation

문제 상황
목표함수의 그래디언트 값을 찾기 위해서는 큐함수 값이 필요하다. 하지만 정책 그래디언트는 가치를 따로 정의하지 않기 때문에 위 식은 계산되어질 수 없다.
REINFORCEMENT
REINFORCEMENT 알고리즘은 큐함수를 반환값 $G_t$로 대체해 정책 그래디언트의 문제를 해결한다.
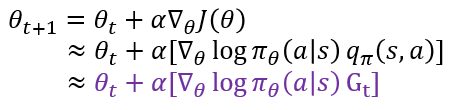
반환값 $G_t$를 얻기 위해서는 에피소드가 종결되어야 한다.
따라서 REINFORCEMENT 알고리즘은 몬테카를로 폴리쉬 그레디언트라고도 불린다.
REINFORCEMENT 구현 포인트
- 오류 함수 :

크로스 엔트로피에서 파생된 형태임으로, 오류 함수로 사용할 수 있다.
- 경사상승법 → 경사하강법
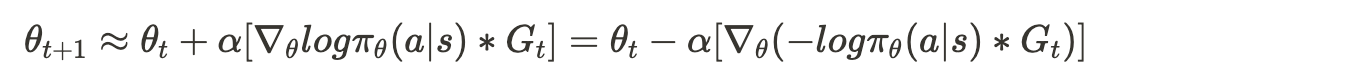
{ % raw %} 기본적으로 REINFORCEMENT은 경사상승법을 사용하지만, $-log \pi_{\theta}(a|s)G_t$의 그래디언트 값을 구한 후 경사하강법을 이용하는 것도 결과적으로 똑같은 결과를 갖는다. 따라서 구현에서는 $log \pi_{\theta}(a|s)G_t$보다 $-log \pi_{\theta}(a|s)G_t$의 그래디언트를 이용한다. { % endraw %}
(+) Actor-Critic
정책 그래디언트는 가치 없이 정책을 근사한다. 하지만 가치가 없기 때문에 누적 보상 함수의 그래디언트 값을 구할 수 없다는 한계가 있다. REINFORCEMENT는 이 큐함수를 반환값으로 대체해 문제를 해결하지만, 이는 에피소드 단위에서만 업데이트가 진행된다는 몬테카를로 접근법의 한계를 갖고 있다. 액터 크리틱은 가치 신경망을 추가해 큐함수 값을 근사하며 해결한다.